Kezdőlap


Feladat:	558. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Faludi Irén , Knuth Előd
Füzet:	1959/november, 137 - 140. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Térgeometria alapjai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/március: 558. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Tekintsük elsőnek a külső érintkezések esetét. Legyen a $k_{1}$ , $k_{2}$ , $k$ körök középpontja rendre $O_{1}$ , $O_{2}$ , $O$ , az első kettő sugara $r_{1}$ , $r_{2}$ , és válasszuk az indexezést úgy, hogy $r_{1} > r_{2}$ ; legyen az $E_{1} E_{2}$ egyenesnek $k_{1}$ , $k_{2}$ -vel való második metszéspontja $E'_{1}$ , $E'_{2}$ , és $O_{1} O_{2}$ -vel való metszéspontja $H_{k}$ . Erről a $H_{k}$ -ról mutatjuk meg, hogy $E_{1} E_{2}$ -nek minden más helyzetén is rajta fekszik.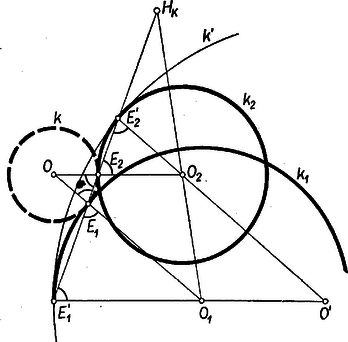

1. ábra

Az érintések folytán az

O_{1}

E_{1}

O

és

O_{2}

E_{2}

O

ponthármasok egy egyenesbe esnek (1. ábra),

E_{1}

E_{2}

elválasztják a középpontokat, ezért

O_{1}

O_{2}

E_{1} E_{2}

-nek ugyanazon partján fekszik, tehát

H_{k}

O_{1} O_{2}

szakaszon kívül van. Az

O_{1} E_{1} E'_{1}

O E_{1} E_{2}

és

O_{2} E'_{2} E_{2}

egyenlő szárú háromszögekből

O_{1} E'_{1} E_{1} ∢ = O_{1} E_{1} E'_{1} ∢ = O E_{1} E_{2} ∢ = O E_{2} E_{1} ∢ = O_{2} E_{2} E'_{2} ∢

, és mivel

E'_{1} E_{1}

és

E_{2} E'_{2}

irányítása egyező, azért

O_{1} E'_{1} ∥ O_{2} E_{2}

, és az

O_{1} E'_{1} H_{k}

O_{2} E_{2} H_{k}

háromszögek hasonlók. Ebből

H_{k} O_{1} : H_{k} O_{2} = E'_{1} O_{1} : E_{2} O_{2} = r_{1} : r_{2} > 1

, tehát

H_{k} O_{1} > H_{k} O_{2}

, vagyis

H_{k}

O_{1} O_{2} = d

szakasznak

O_{2}

-n túli meghosszabbításán fekszik, továbbá (

H_{k} O_{1} - H_{k} O_{2}) : H_{k} O_{2} = d : H_{k} O_{2} = (r_{1} - r_{2}) : r_{2}

alapján

H_{k}

-nak

O_{2}

-től való távolsága

H_{k} O_{2} = d r_{2} / (r_{1} - r_{2})

, és ez valóban független

k

-tól. Másrészt

O_{1} E'_{1}

és

O_{2} E_{2}

irányítása is egyező, tehát

E'_{1} E_{2}

k_{1}

k_{2}

körök egy-egy párhuzamos és egyirányú sugarának végpontjait összekötő egyenes,

H_{k}

pedig ennek a körök centrálisával való metszéspontja, vagyis a két kör külső hasonlósági pontja.
Ugyanígy bizonyítjuk az állítást, ha a változó kör

k_{1}

és

k_{2}

mindegyikével belső érintkezésben van (1. ábra

k'

köre, ennek ‐ hogy ábránk ne váljék zsúfolttá, azt választottuk, amelynek érintési pontjai éppen

E'_{1}

E'_{2}

; a bizonyítás megfordításából kiderül, hogy ilyen kör van). A meggondolás bevezető része így módosul:

O_{1}

ugyanazon oldalán van

E'_{1}

-nek, mint

O'

, ugyanígy áll

O_{2}

E'_{2}

-höz képest, ezért

O_{1}

O_{2}

ismét ugyanazon oldalán van

E'_{1} E'_{2}

nek, ismét az

O_{1} O_{2}

szakaszon kívül fekvő

H_{k}

-ra jutunk. (Az ábrán

k_{1}

és

k_{2}

, valamint az

r'

sugarú

k'

belső érintkezése olyan, hogy

k'

magába foglalja az adott köröket:

r' > r_{1} > r_{2}

; meggondolásunk azonban

r_{2} < r' < r_{1}

és

r' < r_{2}

esetén is érvényes.)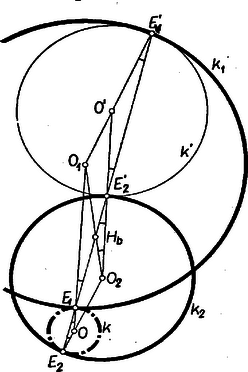

2. ábra

Hasonlóan bizonyítható a vegyesen külső és belső érintkezések esete is (a 2. ábra ismét két ilyet mutat; ezekben is az

E

és

E'

pontok szerepe felcserélődik, a

k

kör

k_{1}

-et kívülről,

k_{2}

-t belülről érinti és benne van

k_{2}

-ben,

k'

pedig benne van

k_{1}

-ben és kívülről érinti

k_{2}

-t). A bizonyítás annyiban módosul, hogy

H_{k}

megfelelője:

H_{b}

O_{1} O_{2}

szakaszon van, ugyanis

O

E_{1}

-nek ellentétes oldalán van mint

O_{1}

, és

E_{2}

-nek ugyanazon oldalán, mint

O_{2}

, ezért

O_{1}

és

O_{2}

E_{1} E_{2}

-nek ellentétes oldalán feküsznek, másrészt hogy a hasonló háromszögek

H_{b}

-nél fekvő szögei csúcsszögek; végül

H_{b} O_{2} = d r_{2} / (r_{1} + r_{2})

, ami ismét állandó.

H_{b}

a két kör belső hasonlósági pontja.
Ha az

E'_{1}

E'_{2}

,,második'' metszéspontok egybeesnek

E_{1}

, ill.

E_{2}

-vel, akkor a szereplő egyenlő szárú háromszögek elfajulnak, mert az alapjukon fekvő szögek

90^{\circ}

-osak lennének, ilyenkor

k

is elfajul

k_{1}

és

k_{2}

-nek valamelyik közös érintőjébe. Akkor is szakasszá fajulnak a szereplő egyenlő szárú háromszögek, sőt a két hasonló háromszög is, ha

O

rajta van az

O_{1} O_{2}

egyenesen; ilyenkor

E_{1}

E_{2}

is az

O_{1} O_{2}

-n van, tehát

E_{1} E_{2} \equiv O_{1} O_{2}

, átmegy

H_{k}

-n és

H_{b}

-n. Ha

O_{2}

egybeesik

O_{1}

-gyel, akkor

H_{k} \equiv H_{b} \equiv O_{1}

.
Ha már most

r_{1} = r_{2}

, akkor kiindulási ábránk

O_{1} O_{2}

-re és felező merőlegesére tükrös, a ,,külső-külső'' és ,,belső-belső'' esetekben

H_{k}

nem létezik,

E_{1} E_{2}

párhuzamos

O_{1} O_{2}

-vel; a többi esetek

H_{b}

pontja ilyenkor az

O_{1} O_{2}

felezőpontjába esik. Ezek az

O_{2} H_{k}

, ill.

O_{2} H_{b}

képletből is kiolvashatók, az előbbi

r_{1} - r_{2} = 0

miatt értelmetlenné válik.
Összefoglalva: az

E_{1} E_{2}

egyenes a

k_{1}

k_{2}

körök külső, ill. belső hasonlósági pontján megy át aszerint, hogy

k

-nak a

k_{1}

és

k_{2}

-vel való érintkezése megegyező, ill. ellentétes értelmű.

Knuth Előd (Budapest, I. István g. II. o. t.)

II. megoldás: Az állítást ábránknak térbeli értelmezést adva bizonyítjuk be. Állítsunk

k_{1}

k_{2}

k

-ra egyenlő nyílásszögű (más szóval hasonló)

K_{1}

K_{2}

K

forgáskúpokat, legyenek ezek csúcsai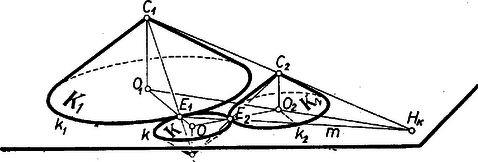

C_{1}

C_{2}

C

A kúpok csúcsát ábránk

S

síkjának alkalmas oldalára téve elérhetjük, hogy

K

egy-egy alkotója egybeesik

K_{1}

, ill.

K_{2}

egy alkotójával, és a kúpok a közös alkotó mentén érintik is egymást. Éspedig ha két körünk között külső érintkezést kívánunk, akkor kúpjaik csúcsát

S

két ellentétes oldalára tesszük (ilyenkor az alkotószakaszokhoz hozzágondoljuk

S

-en túl való folytatásukat, az alkotók tehát a csúcsból kiinduló félegyenesek), belső érintkezésük esetén pedig

S

-nek ugyanazon oldalára kerülnek a csúcsok (ilyenkor elég alkotószakaszra gondolni). Elsőnek pl.

K

és

K_{1}

-et helyezzük el, majd

K_{2}

-t a

K

-hoz viszonyítva. Így eredeti ábránk körei a kúpoknak

S

-sel való metszésvonalai, mindegyik középpont a megfelelő

C

-nek

S

-en való vetülete, az

O O_{1}

és

O O_{2}

egyenesek a közös alkotók vetületei,

E_{1}

és

E_{2}

pedig a közös alkotóknak

S

-en való döféspontjai. Most már láthatjuk, hogy ezen alkotók egybeesését (a csúcsok elhelyezésén felül) egyrészt az biztosítja, hogy minden alkotó ugyanakkora szöggel hajlik

S

-hez, másrészt az, hogy benne vannak az

O O_{1}

-en,

O O_{2}

-n át

S

-re merőlegesen álló síkban.
Most már a vizsgálandó

E_{1} E_{2}

egyenes a közös alkotók

T

síkjának (másképpen: a

C_{1}

C_{2}

C

csúcsokkal meghatározott síknak)

S

-sel való

m

metszésvonala.

T

-ben benne fekszik a

C_{1} C_{2}

egyenes is, ezért ennek

S

-sel való

H

döféspontja

m

-en fekszik. Ha

k

és vele

E_{1} E_{2}

a követelményeknek megfelelően változik, akkor

T

C_{1} C_{2}

egyenes körül elfordulva más-más helyzetet vesz fel, de állandóan átmegy

H

-n, és így ugyanez áll

m

-re is. ‐ Amíg

k_{1}

és

k_{2}

sugarai különbözők, addig

C_{1}

és

C_{2}

S

-től különböző távolságban vannak, ezért

H

biztosan létezik. Ha a sugarak egyenlők, és

K_{1}

és

K_{2}

S

-nek ugyanazon oldalára kerültek (a ,,belső-belső'' és a ,,külső-külső'' eset), és ezért

C_{1} C_{2}

párhuzamos

S

-sel, ebben az esetben ‐ és csak ebben ‐

H

nem létezik, az

E_{1} E_{2}

egyenesek párhuzamosak

C_{1} C_{2}

-vel és így egymással.

Faludi Irén (Budapest, Ságvári E. gyak. lg. II. o. t.)