Kezdőlap


Feladat:	549. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Sasi Éva
Füzet:	1959/november, 131 - 132. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/február: 549. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek az $A_{1} B_{1} C_{1} = H_{1}$ háromszög szögei rendre $α$ , $β$ , $γ$ , és legyen $α \geq 120^{\circ}$ , továbbá $β \geq γ$ . A bizonyítást a következő esetek vizsgálatára bontjuk fel: 1) 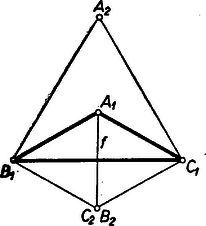$α = 120^{\circ}$ , $β = γ (= 30^{\circ})$ ; 2) $α = 120^{\circ}$ , $β > γ$ ; 3) $α > 120^{\circ}$ , $β \geq γ$ .

1. ábra

Az 1) és 2) esetekben a

B_{2} A_{1} C_{1} ∢ = C_{2} A_{1} B_{1} ∢ = 60^{\circ}

-os szögek

B_{2} A_{1}

C_{2} A_{1}

szára egybeesik a

B_{1} A_{1} C_{1}

szög

f

(belső) szögfelezőjével, és így egymással is. Az 1) esetben

H_{1}

egyenlő szárú, így

B_{2} A_{1} = C_{1} A_{1} = B_{1} A_{1} = C_{2} A_{1}

, így

B_{2}

egybeesik

C_{2}

-vel, ami megfelel a bizonyítandó állításnak.
A továbbiakban feltesszük, hogy

H_{1}

betűzése pozitív körüljárású, vagyis pl. az

A_{1} B_{1}

félegyenest

A_{1}

körül

A_{1} C_{1}

-be az óramutató járásával ellentétes irányú,

180^{\circ}

-nál kisebb forgás viszi át. ‐ A 2) esetben

A_{1} C_{1} > A_{1} B_{1}

, így

f

-en a pontok sorrendje:

A_{1}

C_{2}

B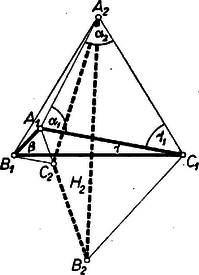_{2}

(2. ábra).

2. ábra

Elegendő megmutatnunk, hogy

A_{2}

ugyanazon partján fekszik

f

-nek, mint

C_{1}

. Ekkor ugyanis az

A_{2} B_{2} C_{2} = H_{2}

háromszög körüljárása megegyezik a

C_{1} B_{2} C_{2}

háromszögével, ez ismét egyezik

C_{1} B_{2} A_{1}

-ével, ez pedig

C_{1} B_{1} A_{1}

-ével, vagyis az

A_{1}

C_{1}

B_{1}

körüljárással,

H_{1}

ellentétes irányú körüljárásával, ami megfelel az állításnak. ‐

A_{1}

B_{1} C_{1} A_{2}

háromszög belsejében van, mert

B_{1} C_{1}

-nek ugyanazon partján fekszik, mint

A_{2}

és

C_{1} B_{1} A_{1} ∢ = β < 60^{\circ} = C_{1} B_{1} A_{2} ∢

, és

A_{1} C_{1} B_{1} ∢ = γ < 60^{\circ} = A_{2} C_{1} B_{1} ∢

. Közelebbről

A_{1} B_{1} < A_{1} C_{1}

folytán

B_{1} C_{1}

felező merőlegesének, vagyis a

B_{1} A_{2} C_{1}

szög felezőjének

C_{1}

-gyel ellentétes partján van

A_{1}

, ezért az

A_{1} A_{2} C_{1} ∢ = α_{2}

szög nagyobb a

B_{1} A_{2} C_{1}

szög felénél,

30^{\circ}

-nál. Másrészt

γ < β

és

γ + β = 60^{\circ}

folytán

γ

kisebb

30^{\circ}

-nál, az ezt

60^{\circ}

-ra kiegészítő

A_{2} C_{1} A_{1} ∢ = γ_{1}

szög pedig nagyobb

30^{\circ}

-nál. Így az

A_{1} C_{1} A_{2}

háromszögből a

C_{1} A_{1} A_{2} ∢ = α_{1} = 180^{\circ} - α_{2} - γ_{1}

szög kisebb

120^{\circ}

-nál. Megmutatjuk még, hogy a

B_{2} A_{1} C_{1}

és

C_{1} A_{1} A_{2}

szögek forgása egyirányú, vagyis

A_{1} B_{2}

-t

A_{1}

körül,

A_{1} C_{1}

-en át

180^{\circ}

-nál kisebb forgás viszi át

A_{1} A_{2}

-be. A

B_{2} A_{1} A_{2}

forgás ezek összege:

B_{2} A_{1} A_{2} ∢ = 60^{\circ} + α_{1} < 180^{\circ}

. Valóban, mindkét forgás pozitív, ugyanis az

A_{1} B_{2} C_{1}

háromszög egyező körüljárású

H_{1}

-gyel, mert

B_{1}

és

B_{2}

A_{1} C_{1}

-nek ugyanazon partján vannak, másrészt az

A_{1} C_{1} A_{2}

háromszög egyező körüljárású

B_{1} C_{1} A_{2}

-vel, ez pedig

B_{1} C_{1} A_{1}

-gyel,

H_{1}

-gyel. Ezzel megmutattuk az állítás helyességét a 2) esetre.
A 3) esetre megmutatjuk, hogy a

B_{2} A_{2}

félegyenest

B_{2}

körül

B_{2} C_{2}

-be pozitiv,

180^{\circ}

-nál kisebb forgás viszi át, tehát a

B_{2} A_{2} C_{2}

körüljárás pozitív.

3. ábra

Ehhez a 2) eset eredményeiből átvehetjük, hogy a

B_{2} A_{1} A_{2}

szög pozitív,

180^{\circ}

-nál kisebb forgás, ugyanis

γ + β < 60^{\circ}

és

γ \leq β

folytán is áll

γ < 30^{\circ}

. Eszerint az

A_{1} B_{2} A_{2}

körüljárás pozitív,

B_{2} A_{2}

-t,

B_{2} A_{1}

-be pozitív forgás viszi át. E forgás szöge kisebb

60^{\circ}

-nál, mert

α_{2} < 60^{\circ}

;

γ_{1} < 60^{\circ}

, így

α_{1} > 60^{\circ}

, és

B_{2} A_{1} A_{2} ∢ > 120^{\circ}

. ─ Másrészt az

A_{1} C_{2} B_{2}

körüljárás is pozitív, mert a

C_{2} A_{1} B_{2}

forgás pozitív, a

120^{\circ}

-nál nagyobb pozitív

B_{1} A_{1} C_{1}

forgás maradványa a kétszeri,

60^{\circ}

-kal való csökkentés után. Ezért az

A_{1} B_{2} C_{2}

forgás pozitív, éspedig kisebb

90^{\circ}

-nál, mert az

A_{1} C_{2} B_{2}

háromszögben

A_{1} C_{2} = A_{1} B_{1} \leq A_{1} C_{1} = A_{1} B_{2}

, vagyis az

A_{1} C_{2} B_{2}

háromszögben van az

A_{1} B_{2} C_{2}

szögnél nagyobb vagy vele egyenlő szög is. Ezek szerint

A_{2} B_{2} C_{2} ∢ = A_{2} B_{2} A_{1} ∢ + A_{1} B_{2} C_{2} ∢ < 150^{\circ} < 180^{\circ}

, amit bizonyítani akartunk.
Mindezzel az állítást minden lehetséges esetben bebizonyítottuk.

Sasi Éva (Makó, József A. g. II. o. t.)