Kezdőlap


Feladat:	541. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bácsy Zs. , Balkay Sarolta , Biborka T. , Bollobás B. , Dömötör Gy. , Endreffy Z. , Faludi Irén , Farkas Z. , Fekete J. , Fritz József , Gagyi Pálffy A. , Gálfi l. , Gáspár R. , Gergelics L. , Grünner Gy. , Gyaraki K. , Horváth Dénes , Horváth Kálmán , Horváth Zalán , Jakabffy I. , Kelen A. , Kerényi Ilona , Kéry G. , Klimó J. , Krámli A. , Kugler Emese , Máté Eörs , Molnár Emil , Móricz L. , Nagy Dezső , Náray Szabó G. , Nováky B. , Opálény M. , Pellionisz A. , Pinkert A. , Piroska Z. , Pollai Marion , Salamin P. , Szalay G. , Székely J. , Szidarovszky Ágnes , Szőts M. , Tomcsányi Gy. , Tóth Vilmos , Zalán P. , Zaránd R.
Füzet:	1959/november, 124 - 128. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1959/január: 541. matematika gyakorlat

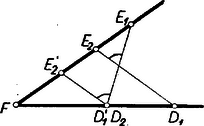
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Menjünk végig a kérdéseken hegyesszögű háromszög esetén, vagyis legyen egyelőre $γ \leq β \leq α < 90^{\circ}$ . Így a magasságtalppont minden oldalszakaszon belső pont, az oldalnak arra a felére esik, amelyiknek a végpontjában a háromszögnek nagyobb szöge van, és a felezőponttal akkor és csak akkor esik egybe, ha az oldal végpontjainál egyenlő szögek vannak. Ugyanis pl. az $A B$ oldal végpontjainál levő $α$ és $β$ hegyes szögek nem közös szárai csak abban az $I$ síksávban metszhetik egymást (1. ábra), amelyet az $A B$ -re $A$ és $B$ -ben állított $b^{*}$ , $a^{*}$ merőlegesek határolnak, hiszen az ezeken túl fekvő $I I$ , ill. $I I I$ félsíkokban az $A C$ , ill. $B C$ szárnak nincs pontja.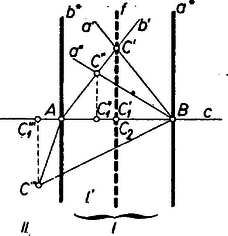

1. ábra

Ennélfogva

C_{1}

valóban

A B

-re esik. Ha

B C = A C

, azaz

α = β

, akkor

C

(az ábrán

C'

ilyen) az

I

sáv tengelyén,

A B

-nek

f

felező merőlegesén van, így

C'_{1} \equiv C_{2}

;

B C > A C

azaz

α > β

esetén pedig

C

(az ábrán

C''

ilyen) az

f

és

b^{*}

közti

I'

sávban van, így

C_{1}

valóban az

A C_{2}

szakaszra, a nagyobb szög oldalára esik. Mivel nekünk az oldalfelező pontot kell viszonyítanunk a magasságtalpponthoz, azért megállapításunkat így mondhatjuk ki: az oldalfelező pont a magasságtalpponttal kettévágott oldalnak a kisebb szög csúcsa felé eső szakaszán van, vagy egybeesik a talpponttal.
Így az előírt

U_{I}

útvonalon visszafordulás nincs.

A_{2}

és

A_{1} C

szakaszon van,

B_{2}

C B_{1}

-en,

C_{2}

C_{1} B

-n, a pontok sorrendjét általában a 2. ábra mutatja.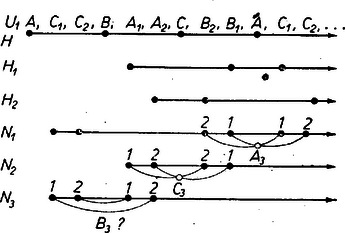

2. ábra

Egybeesések:

α = β

esetén

C_{2} \equiv C_{1}

β = γ

esetén

A_{2} \equiv A_{1}

α = β = γ

esetén e kettőn felül még

B_{2} \equiv B_{1}

, (vagyis

B_{2} \equiv B_{1}

csak egyenlő oldalú háromszögben áll fenn).
Esetünkben

U_{I}

azonos az

A B C = H

háromszög kerületének bejárásával. Az

A_{1} B_{1} C_{1} = H_{1}

és

A_{2} B_{2} C_{2} = H_{2}

háromszögek körüljárása viszont

U_{I}

olyan rövidítése, amelyben

H

csúcsait

H_{1}

, ill.

H_{2}

oldalaival ,,átvágjuk'', az oldalakból csak egy (belső) pontot hagyva meg, ezért

H

H_{1}

és

H_{2}

körüljárási iránya megegyező.
Ha

H_{1}

és

H_{2}

-nek egy csúcsa sem közös, tehát

γ < β < α < 90^{\circ}

(amiből

α > 60^{\circ}

γ < 60^{\circ}

), akkor a vizsgálandó egyenespárok tagjai különbözők. A

B_{1} C_{2}

és

C_{1} B_{2}

egyenesek biztosan metszik egymást egy a

H

-n belül fekvő

A_{3}

pontban (3. ábra), mert ezek az

N_{1} = C_{1} C_{2} B_{2} B_{1}

négyszög átlói, és e négyszög konvex, mert a kerülete ugyancsak átvágásos rövidítése

U_{I}

-nek (lásd a 2. ábra vázlatát), márpedig konvex négyszög átlói a négyszög belsejében metszik egymást.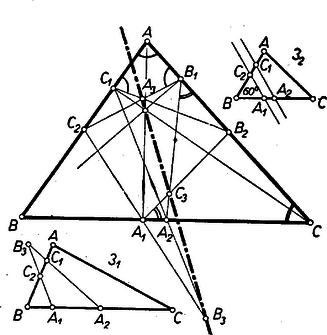

3. ábra

Ugyanígy adódik az

N_{2} = A_{1} A_{2} B_{2} B_{1}

konvex négyszögből, hogy

A_{1} B_{2}

és

B_{1} A_{2}

-nek

C_{3}

metszéspontja is létezik, éspedig

H

-n belül. A

C_{1} A_{2}

és

A_{1} C_{2}

pár tagjai viszont az

N_{3} = C_{1} C_{2} A_{1} A_{2}

konvex négyszögben szemben fekvő oldalegyenesek, így csak

H

-n kívül lehet közös pontjuk; ezt ‐ ha létezik, ‐

B_{3}

-mal jelöljük.
A

B_{1} C_{2}

C_{1} B_{2}

egyenespár

B_{1} A_{3} C_{1}

szögét az

N_{4} = A C_{1} A_{3} B_{1}

négyszögből számíthatjuk. Mindegyik magasságtalppont a megfelelő oldal fölé írt Thalész-körön van, ezért pl.

A_{1} C_{2} = B_{1} C_{2} = A B / 2

. Így az

A B_{1} C_{2}

A C_{1} B_{2}

háromszögek egyenlő szárúak,

A

-nál fekvő szögük közös:

α

, ezért

B_{1}

-nél,

C_{1}

-nél fekvő szögük is

α

. Ennélfogva

N_{4}

-ből az a

B_{1} A_{3} C_{1}

szög, amelynek terében

A

fekszik,

360^{\circ} - 3 α

-val egyenlő (ez

90^{\circ}

és

180^{\circ}

közé eső szög). Másképpen:

A_{3}

-ból a

B_{1} B_{2}

és

C_{1} C_{2}

szakaszok látószöge

180^{\circ} - (360^{\circ} - 3 α) = 3 α - 180^{\circ}

(

0^{\circ}

és

90^{\circ}

közé eső szög).
Kézenfekvő volna innen minden

A

B

C

, valamint az

α

betű helyére rendre

C

A

B

γ

-t írva, az indexeket pedig meghagyva ezt kimondani: ,,

C_{3}

-ból

A_{1} A_{2}

és

B_{1} B_{2}

látószöge

3 γ - 180^{\circ}

''. Ez azonban

γ < 60^{\circ}

folytán negatív szög. Hasonlóan ,,szokatlan'' eredményt ad a megelőző megállapítás ,,átírása'' : ,,az az

A_{1} C_{3} B_{1}

szög, amelynek terében

C

fekszik,

360^{\circ} - 3 γ

-val egyenlő'', ‐ ez ugyanis nagyobb

180^{\circ}

-nál. Bár az utóbbit

360^{\circ}

-ra kiegészítő, az

A

-t és

B

-t tartalmazó

A_{1} C_{3} B_{1}

szög már jól szemlélhető, nagysága kivonással

3 γ

-nak adódik, és

0^{\circ} < 3 γ < 180^{\circ}

, mégis joggal kételkedhetünk e ,,homályos'' úton kapott eredményben. ‐ Ezt azonban úgy is megkaphatjuk, ha

C

és

C_{3}

-hoz

A_{2}

és

B_{2}

-t vesszük hozzá, amelyek

U_{I}

szerint közelebb vannak

C

-hez, mint

A_{1}

és

B_{1}

és amelyekkel az

N_{5} = C B_{2} C_{3} A_{2}

négyszög konvex. A

C A_{1} B_{2}

és

C B_{1} A_{2}

egyenlő szárú háromszögekben

C

A_{1}

és

B_{1}

-nél

γ

, ezért

B_{2}

A_{2}

-nél

180^{\circ} - 2 γ

szög fekszik, tehát

N_{5}

-ből

B_{2} C_{3} A_{2} ∢ = 360^{\circ} - γ - 2 (180^{\circ} - 2 γ) = 3 γ

. Eszerint az

A_{1} A_{2}

és

B_{1} B_{2}

szakaszok

C_{3}

-ból vett látószöge

180^{\circ} - 3 γ

. ^{$^{*}$}
Tisztázzuk a

C_{1} A_{2}

A_{1} C_{2}

egyenespár metszéspontjának helyzetét!

B A_{1} C_{2} ∢ = B C_{1} A_{2} ∢ = β

és

B A_{2} C_{1} ∢ = B C_{2} A_{1} ∢ = 180^{\circ} - 2 β

, eszerint

β < 60^{\circ}

esetén az egyeneseknek

A_{1}

A_{2}

-n túli félegyenesei metszik egymást (3. ábra főrésze),

β > 60^{\circ}

esetén a

C_{1}

C_{2}

-n túliak (

3_{1}

mellékábra),

β = 60^{\circ}

esetén pedig a két egyenes párhuzamos (

3_{2}

mellékábra). Ugyanis

β < 60^{\circ}

mellett a két egyenes

B C

-vel, ennek

H

-t tartalmazó partján olyan szögeket alkot, melyeknek összege nagyobb

180^{\circ}

-nál:

C_{2} A_{1} A_{2} ∢ + C_{1} A_{2} A_{1} ∢ = (180^{\circ} - β) + (180^{\circ} - 2 β) = 360^{\circ} - 3 β > 180^{\circ}

, ezért a két egyenes

B C

-nek valóban nem a

H

-t tartalmazó partján metszi egymást;

β > 60^{\circ}

esetén pedig hasonlóan

A_{2} C_{1} C_{2} ∢ + A_{1} C_{2} C_{1} ∢ = β + 2 β = 3 β > 180^{\circ}

. ‐ Ezek szerint

β < 60^{\circ}

esetén az

A_{1} A_{2} B_{3}

háromszög

A_{1}

és

A_{2}

-nél fekvő szögeinek összege

β + 2 β = 3 β

, ezért

B_{3}

-ból

A_{1} A_{2}

és

C_{1} C_{2}

látószöge

180^{\circ} - 3 β

, ill.

β > 60^{\circ}

esetén hasonlóan

3 β - 180^{\circ}

.
A szögekre tett megállapításaink

α = β \neq γ

és

α \neq β = γ

esetén is érvényesek, ilyenkor két egyenespárunk meghatározó pontjaiból egy-egy egybeesik, és

β

nem

60^{\circ}

-os. Egyenlő oldalú háromszögben mindhárom egyenespárunk páronként egybeesik, a szögekre vonatkozó kérdés tárgytalan.
II. Derékszögű háromszög esetén

γ \leq β < α = 90^{\circ}

B_{1}

és

C_{1}

A

csúcsba esnek, de visszafordulás a módosult

U_{I I}

-ben sincs.

H_{1}

egyenesszakasszá fajul, körüljárásáról nem beszélhetünk.

A_{3}

A

-ba esik, így a fentebb használt

N_{4}

ponttá zsugorodik, a

B_{1} C_{2} \equiv A C_{2} \equiv A B

és

C_{1} B_{2} \equiv {A B}_{2} \equiv A C

egyeneseknek, vagyis a befogóknak

90^{\circ}

-os szögét a fenti

360^{\circ} - 3 α

és

3 α - 180^{\circ}

képletek mégis helyesen adják meg. Többi megállapításaink változatlanul átvehetők, mert a hozzájuk vezető meggondolások érvényesek maradnak.
III. Tompaszögű háromszög esetén (

γ \leq β < 90^{\circ} < α

) a két hegyes szög csúcsából húzott magasság,

B_{1}

C_{1}

talppontja az

A C

A B

oldalnak

A

-n túli meghosszabbítására esik, (lásd az 1. ábrán

C'''

-t) így az előírt

U_{I I I}

útvonalon két visszafordulás van, a bejárást újra és újra ismételve

A

-n

3

-szor annyiszor haladunk át, mint

B

-n és

C

-n.

B_{2}

C_{2}

így is

C B_{1}

-en,

C_{1} B

-n van. A pontok sorrendje, a többszörös átmeneteket is jelölve:

A

C_{1}

A

C_{2}

B

A_{1}

A_{2}

C

B_{2}

A

B_{1}

A

C_{1}

...

H_{2}

körüljárása most is átvágásos rövidítése

H

-énak, így körüljárásuk egyező.

H_{1}

körüljárása a kieső pontok miatt nem vezethető le

H

-éból.

H_{1}

körüljárása ellentétes

H

-éval, mert a két kieső talpponttal képezett

A C_{1} B_{1}

háromszög körüljárása egyezik

H

-éval, így ennek

A B_{1} C_{1}

körüljárása ellentétes azokkal,

H_{1}

körüljárása pedig az utóbbival egyező, mert

A_{1}

ugyanazon partján van

B_{1} C_{1}

-nek, mint

A

.
A szögekre vonatkozó vizsgálatot megrövidíthetjük. Fel kell ugyanis figyelnünk arra, hogy eddigi szög-eredményeink rendre csak

α

β

γ

-tól függnek, másrészt hogy a

β ≷ 60^{\circ}

melletti eredmény ‐ bár más-más meggondolással nyertük, azonos a

γ

-ra, ill.

60^{\circ} < α \leq 90^{\circ}

-ra adódott eredménnyel. Vegyük észre, hogy tulajdonképpen a következő kérdést vizsgáltuk több változatban:

D_{2}

E_{2}

az egymást

F

-ben metsző

d

e

egyenesek egy-egy tetszés szerinti, de

F

-től különböző pontja, egy-egy

D_{1}

, ill.

E_{1}

pontjukat pedig az

E_{2}

, ill.

D_{2}

középpontú,

F

-en átmenő körrel metsszük ki, vagyis

D_{1} E_{2} = F E_{2}

E_{1} D_{2} = F D_{2}

; mekkorák a

D_{1} E_{2}

és

E_{1} D_{2}

egyenesek szögei, ha

D_{2} F E_{2} ∢ = φ

. Feladatunk céljára

φ

0^{\circ}

és

180^{\circ}

közti szög, és a

D_{2} F : E_{2} F

arány más-más értéke szerint kapjuk mindazon háromszög alakokat, melyek egyik szöge

φ

; a

φ \leq 90^{\circ}

eseteket azonban már megvizsgáltuk.

Egyszerűbb ez a kérdés, ha

D_{1} E_{2}

helyett a vele

D_{2}

-n át húzott

g

párhuzamost tekintjük, ugyanis

E_{2}

-t

g

és

e

-nek

E'_{2}

metszéspontjával helyettesítve a kérdéses szögek változatlanok, pontjaink száma viszont csökken, mert az

F D_{1} E_{2}

és

F D_{2} E'_{2}

háromszögek hasonlók, és ezért az

E'_{2}

-ből adódó

D'_{1}

azonos

D_{2}

-vel. Ez is mutatja, hogy a keresett szög valóban csak

φ

-től függhet, de a

D_{2} F : E_{2} F

aránytól nem; tehát a tompaszögű háromszög hegyes szögeinek megfelelő

C_{1} A_{2}

A_{1} C_{2}

és

A_{1} B_{2}

B_{1} A_{2}

egyenespárok szögeit nem kell újra megállapítanunk.

E'_{2}

-t

F D_{2}

felező merőlegese metszi ki

e

-ből (hacsak nem

φ = 90^{\circ}

, mert ekkor

E'_{2}

nem létezik), tehát

90^{\circ} < φ < 180^{\circ}

esetén

E'_{2}

φ

szög

F E_{2}

szárának

F

-en túl való meghosszabbításán van. Ez pedig azt jelenti, hogy a

φ

és

180^{\circ} - φ

nagyságú szögekhez ugyanaz az egyszerűsített ábra tartozik, tehát a keresett szög értéke ugyanaz.
Eszerint

90^{\circ} < α < 120^{\circ}

esetén a

B_{1} C_{2}

C_{1} B_{2}

egyenespár szöge akkora, mint a

90^{\circ} > α' = 180^{\circ} - α < 60^{\circ}

-nak megfelelő

α'

esetén:

3 α' - 180^{\circ} = 3 (180^{\circ} - α) - 180^{\circ} = 360^{\circ} - 3 α

;

α = 120^{\circ}

esetén a

B_{1} C_{2}

és

C_{1} B_{2}

egyenesek párhuzamosak; végül

120^{\circ} < α < 180^{\circ}

esetén akkora a szög, mint

60^{\circ} > β' = 180^{\circ} - α > 0^{\circ}

esetén, vagyis

180^{\circ} - 3 β' = 180^{\circ} - 3 (180^{\circ} - α) = 3 α - 360^{\circ}

.
Ezzel vizsgálatunkat befejeztük.

Fritz József (Mosonmagyaróvár, Kossuth L. g. II. o. t.)

Megjegyzések. 1. Az egyszerűsített ábrából a

φ < 90^{\circ}

esetekre is könnyebben kapjuk a keresett szöget. Pl.

0^{\circ} < φ < 60^{\circ}

esetén

F D_{2} E_{1} ∢ = 180^{\circ} - 2 φ > 60^{\circ} > φ

, ezért

F E_{1} > F E_{2}'

, így az

F D_{2} E_{1}

és

F D_{2} E'_{2}

egyenlő szárú háromszögekből

τ = E_{1} D_{2} E'_{2} ∢ = E_{1} D_{2} F ∢ - E'_{2} D_{2} F ∢ = (180^{\circ} - 2 φ) - φ = 180^{\circ} - 3 φ

. Célszerű lett volna tehát a módosított problémát segédtételként előre bizonyítani. Így azonban nem látnók, miért éppen erre a segédtételre van szükség; ezért a fenti nehézkes út mégis tanulságos.
2. A fentiekkel közel járunk egy névtelen levélíró azon javaslatának teljesítéséhez, hogy időnként tegyük közzé egy-egy megoldó közlését arról, hogy ,,hogyan jött rá a megoldásra''.
3. Hogy tompaszögű háromszögben

H_{1}

ellentétes körüljárású

H

-val, azt így is beláthatjuk: Legyen az

A B_{1} B A_{1}

és

A C_{1} C A_{1}

négyszögek átlóinak metszéspontja

B^{*}

C^{*}

. A négyszögek a látottak szerint konvexek, ezért

B^{*}

C^{*}

mindkét átlószakaszon rajta van. Így

H_{1}

körüljárása azonos

A_{1} B^{*} C^{*}

-éval, ez viszont átvágásos rövidítése az

A

C^{*}

C

A_{1}

B

B^{*}

A

útvonalnak, az

A C B

bejárásnak.
4. Olvassuk el a 948. feladathoz fűzött megjegyzés második bekezdését is.

^{$^{*}$}A fenti két meggondolás eltérése a körüljárásból következik; figyeljük meg a 2. ábrán

A

és

C

körül az indexek elhelyezkedését!