Kezdőlap


Feladat:	533. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	, Budai Katalin , Jójárt István , Krámli András , Ruda Győző
Füzet:	1959/szeptember, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Trigonometria, Háromszögek nevezetes tételei, Trapézok, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/december: 533. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a $R$ sugarú kör középpontja $O$ , a beleírt szabályos ötszög egy oldala $A B$ , és ennek felezőpontja $C$ ; így $A O B ∢ = 360^{\circ} / 5 = 72^{\circ}$ , $A O C ∢ = C O B ∢ = 72^{\circ} / 2 = 36^{\circ}$ , és a beírt kör középpontja 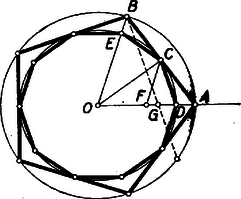$O$ , sugara $O C = r$ .

Vegyük

C

-t a beírt szabályos tízszög egy csúcsának, ekkor a vele szomszédos

D

E

csúcsokat

O A

O B

metszi ki az

r

sugarú körből, mert így

C O D ∢ = C O E ∢ = C O A ∢ = 360^{\circ} / 10 = 36^{\circ}

, tehát

C D

C E

valóban oldalai a tízszögnek. Legyen végül

O A

felezőpontja

F

, tehát

O F = F A

F

egyszersmind középpontja az

O A C

derékszögű háromszög körülírt körének, tehát

F C = F O

. Így az

O C F

háromszög egyenlő szárú, és

F

-nél fekvő külső szögére

D F C ∢ = 2 F O C ∢ = 2 D O C ∢ = 72^{\circ}

. Másrészt az

O C D

háromszögből

O D C ∢ = (180^{\circ} - 36^{\circ}) / 2 = 72^{\circ}

, így

F D C ∢ = D F C ∢

, a

C D F

háromszög egyenlő szárú, tehát

C D = C F = O F = R / 2

, amit bizonyítanunk kellett.

Jójárt István (Esztergom, Ferences g. I. o. t.)

II. megoldás: Az I. megoldás jelöléseivel

C

, ill.

F

felezi az

O A B

háromszög

A B

, ill.

A O

oldalát, ezért

C F

párhuzamos

O B

-vel, az

O E C F

négyszög trapéz. Benne ‐ a fentiekhez hasonlóan ‐

C E O ∢ = E O F ∢ = 72^{\circ}

, így a trapéz egyenlő szárú, tehát

C E = F O = R / 2

Budai Katalin (Budapest, Berzsenyi D. lg. II. o. t.)

Megjegyzések. 1. Lényegében ugyanezeket a tényeket használjuk ki, ha a

C D

-vel

B

-n át húzott párhuzamosnak

O A

-val való metszéspontját

G

-vel jelölve azt mutatjuk meg, hogy az

O B G

háromszög egyenlő szárú, és így

O B = B G = 2 C D

Ruda Győző (Budapest, Kőrösi Csoma S. g. II. o. t.)

2. Az állítást a szabályos ötszög oldala és a köréje, ill. beléje írható kör sugara, valamint a szabályos tízszög oldala és a köréje írható kör sugara között fennálló (könnyen megállapítható) arányok alapján is bizonyíthatjuk. Ezek az arányok egyszerű kapcsolatban állnak

18^{\circ}

és

36^{\circ}

szinuszával és koszinuszával,

Krámli András (Szeged, Radnóti M. g. II. o. t.)