Kezdőlap


Feladat:	517. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Bollobás Béla , Szendrői Csaba
Füzet:	1959/május, 144 - 146. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/október: 517. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $A B E$ , $A D F$ , $C B G$ és $C D H$ háromszögek szerkesztésüknél fogva derékszögűek és egyenlő szárúak, így $A$ , $B$ , $C$ , $D$ -nél fekvő szögeik $45^{\circ}$ -osak. Ezért az $A$ , $E$ , $F$ , az $E$ , $B$ , $G$ , a $G$ , $C$ , $H$ és a $D$ , $H$ , $F$ ponthármasok egy-egy egyenesbe esnek. Továbbá ennek a négy egyenesnek mindegyike merőleges a következőre és az utolsó az elsőre. Ennélfogva az $E F H G$ négyszög derékszögű.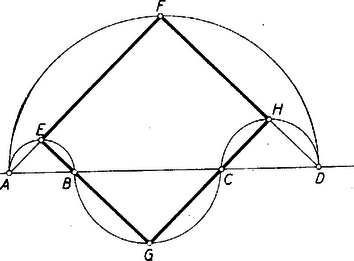

1. ábra

Legyen az

A B

C B

és

C D

szakaszok hossza rendre

2 e

2 f

2 g

; így

A D = 2 (e + f + g)

. Ekkor négyszögünk oldalai:

E G = E B + B G = \sqrt[]{2} e + \sqrt[]{2} f = \sqrt[]{2} (e + f)

és

G H = G C + C H = \sqrt[]{2} f + \sqrt[]{2} g = \sqrt[]{2} (f + g)

. Ezekből a területe:

\begin{matrix} t_{1} = E G \cdot G H = 2 (e + f) (f + g) \end{matrix}

Másrészt félköreink sugarai rendre

e

e + f + g

f

g

. Az általuk bezárt területet úgy kapjuk, hogy az

A D

és

C B

átmérő fölötti félkörök területének összegéből kivonjuk az

A B

és

C D

átmérő fölötti félkörök területének összegét. Az

π / 2

közös tényezőt mindjárt kiemelve:

\begin{matrix} t_{2} = [{(e + f + g)}^{2} + f^{2} - e^{2} - g^{2}] π / 2. \end{matrix}

(1)

Alakítsuk szorzattá a zárójelben az első és harmadik, valamint a második és a negyedik tagot, majd emeljük ki az adódó

(f + g)

közös tényezőt. Így

\begin{matrix} t_{2} = [(2 e + f + g) (f + g) + (f - g) (f + g)] π / 2 = \\ = (2 e + f + g + f - g) (f + g) π / 2 = (e + f) (f + g) π . \end{matrix}

A két terület aránya:

t_{1} : t_{2} = 2 : π

, és ez valóban független az

A B

B C

C D

szakaszok hosszától.

Szendrői Csaba (Sopron, Kempelen F. Gépip. t. II. o. t.)

II. megoldás: Az I. megoldást, miután megállapítjuk, hogy a négy ponthármas egy-egy egyenesen van, így is folytathatjuk. Az

E F H G

négyszög

t_{1}

területét úgy kaphatjuk, hogy az

A D F

és

B C G

egyenlő szárú derékszögű háromszögek területének összegéből kivonjuk az

A B E

és

C D H

egyenlő szárú derékszögű háromszögek területének összegét. Jelöljük ezeket általában

t (c)

-vel,

c

helyére mindig a megfelelő átfogót írva. Ekkor

\begin{matrix} t_{1} = t (A D) + t (B C) - t (A B) - t (C D) . \end{matrix}

Hasonlóan összeadásokkal és kivonással kapjuk a görbevonalú idom területét a szóban forgó félkörök területéből. Jelöljük a

c

átmérőjű félkör területét

T (c)

-vel így:

\begin{matrix} t_{2} = T (A D) + T (B C) - T (A B) - T (C D) . \end{matrix}

Már most általában:

\begin{matrix} t (c) : T (c) = \frac{c^{2}}{4} : \frac{c^{2} π}{8}, és így t (c) = \frac{2}{π} T (c) . \end{matrix}

Ennek alapján

\begin{matrix} t_{1} = \frac{2}{π} T (A D) + \frac{2}{π} T (B C) - \frac{2}{π} T (A B) - \frac{2}{π} T (C D) = \frac{2}{π} t_{2}, tehát \frac{t_{1}}{t_{2}} = \frac{2}{π} . \end{matrix}

Evvel az állítást bebizonyítottuk.

Bollobás Béla (Bp. V., Apáczai Csere J. Gyak. g. II. o. t.)

Megjegyzések. 1. A II. megoldás gondolatával és az I. megoldás jelöléseivel

\begin{matrix} t_{1} = \frac{1}{4} [{(2 e + 2 f + 2 g)}^{2} + {(2 f)}^{2} - {(2 e)}^{2} - {(2 g)}^{2}] = \\ {(e + f + g)}^{2} + f^{2} - e^{2} - g^{2} \end{matrix}

és ez (1)-gyel egybevetve átalakítás nélkül vezet a kívánt eredményhez.
2. A feladat állítását többféleképpen is lehet általánosítani.
Akkor is érvényes az állítás, ha egyenlő szárú derékszögű háromszögek helyett olyan hasonló és azonos körüljárási értelmű

A B E

A D F

C B G

C D H

háromszögeket írunk az

A B

A D

C B

C D

szakaszokra, amelyeknek e szakaszok megfelelő oldalai, a félkörívek helyett viszont a háromszögek köré írt körnek az

E

F

G

H

csúcsot tartalmazó

A B

A D

C B

C D

ívét (2. ábra).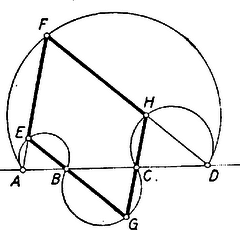

2. ábra

Ha az

A

B

C

D

pontok sorrendje más, akkor amely szakasz végpontjai az eddigivel szemben fordított sorrendben következnek egymásra, arra a félkört az egyenesnek az eddigivel átellenes oldalán írva ugyancsak érvényes marad az állítás. Ha ilyenkor a

4

félkör

4

csúcsot alkot, akkor a görbevonalú idom két részből áll (3‐4. ábrák).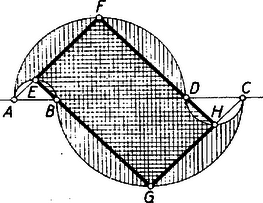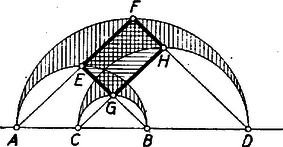

3. ábra

4. ábra