Kezdőlap


Feladat:	511. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Fejes Gy. , Kartaly F. , Kéry G. , Miklós A. , Nagy Márton , Náray-Szabó G. , Padányi P. , Palágyi F. , Palka I. , Pallós L. , Piroska Z. , Ruda Gy. , Simai L. , Zakariás I.
Füzet:	1959/április, 103 - 105. oldal		PDF \| MathML
Témakör(ök):	Magasságvonal, Feuerbach-kör, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/szeptember: 511. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás: Legyen $A B C$ egy az előírásoknak megfelelő háromszög; az adott talppontok legyenek az $a = B C$ és $b = C A$ -ra merőleges magasságok $A_{1}$ , ill. $B_{1}$ talppontjai, továbbá legyen adott az $A A_{1}$ magasság és a $C A$ oldal közti $C A A_{1}$ szög, jelöljük ezt $δ$ -val. Feltehetjük, hogy $A_{1}$ és $B_{1}$ különbözők, $δ$ egy $0^{\circ}$ -tó1 különböző hegyes szög, és $A B C ∢ \neq 90^{\circ}$ ; egyrészt ugyanis a három kizárt feltétel bármelyikéből következik, hogy a másik kettő is teljesül, és akkor minden olyan derékszögű háromszög megfelel a követelményeknek, melynek derékszögű csúcsa az adott $A_{1} \equiv B_{1} \equiv C$ pont, másrészt egy háremszögben egy magasság az ezzel közös csúcsból induló oldalakkal hegyesszöget zár be, tehát $δ < 90^{\circ}$ kell hogy legyen.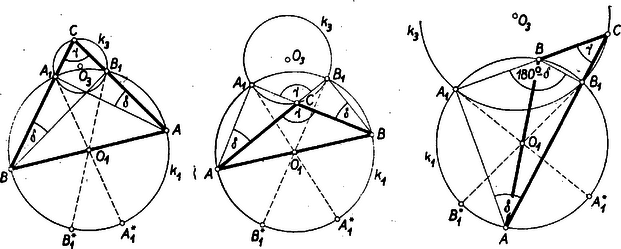
Az $A_{1}$ , $B_{1}$ talppontok az $A B$ oldal fölé írt Thales-körön vannak, mégpedig az $A B$ egyenes egy oldalán vagy ellenkező oldalán, aszerint, amint az $A B C$ háromszögben sem $A$ -nál, sem $B$ -nél nincs tompaszög, vagy az egyik szög tompa. Az első esetben az $A_{1} B_{1}$ szakasz $A$ -ból is, $B$ -ből is $δ$ szög alatt látszik, a második esetben a két csúcs egyikéből $δ$ , a másikéból $180^{\circ} - δ$ szög alatt. (Ha pl. $A$ egybeesik $B_{1}$ -gyel, akkor az egyik látószög nem létezik.) Mivel $A_{1} B_{1}$ és $δ$ adott, ezek meghatározzák a kör sugarát. $A$ és $B$ számára két ilyen $k_{1}$ és $k_{2}$ kör felel meg, amelyek egymás tükörképei az $A_{1} B_{1}$ egyenesre; a rajzokon csak az egyiket tüntettük fel. Nem kapunk azonban valódi háromszöget, ha $A$ egybeesik $A_{1}$ -gyel, és így $B$ az ezzel átellenes $A_{1}^{*}$ pontba kerül, vagy ha $B$ esik $B_{1}$ -be, tehát ha $A$ az ezzel átellenes $B_{1}^{*}$ -gal esik egybe.

Ha most már felvesszük

A

-t tetszés szerint, csak

A_{1}

- től és

B_{1}^{*}

-tól különbözőnek

k_{1}

-en, ez egyértelműen meghatározza a háromszöget:

B

k_{1}

kör

A

-val átellenes pontja,

C

pedig az

A B_{1}

és

B A_{1}

egyenesek metszéspontja, ha

A ≢ A_{1}^{*}

. Ha

A \equiv A_{1}^{*}

, tehát

B \equiv A_{1}

, akkor a

B C

oldalegyenest mint az

A A_{1} \equiv A B

magasságra az

A_{1} \equiv B

pontban merőleges egyenest kapjuk meg.
Ha a

C

metszéspont a

k_{1}

körön kívül van, akkor

A_{1}

γ = A C B

szögnek

C B

szárára (a

C B

szakaszra vagy

B

-n túli meghosszabbítására) esik, és így

γ

A A_{1} C

derékszögű háromszög hegyesszöge, amiből

γ = 90^{\circ} - δ

. Ha viszont

C

k_{1}

körbe esik, akkor

A_{1}

C B

szár

C

-n túli meghosszabbítására esik. Így

γ

A A_{1} C

háromszög külső szöge, tehát

γ = 90^{\circ} + δ

. Ezek szerint

C

olyan,

A_{1}

-en és

B_{1}

-en átmenő körön van, amelynek a pontjaiból az

A_{1} B_{1}

szakasz

90^{\circ} - δ

, vagy

90^{\circ} + δ

szögben látszik.
Ilyen kör kettő van,

k_{3}

és

k_{4}

, egymásnak tükörképei az

A_{1} B_{1}

-re. Megmutatjuk, hogy ha

A

-t a

k_{1}

-en választjuk, akkor

C

azon a

k_{3}

-on van, amelynek

O_{3}

középpontja

A_{1} B_{1}

-nek ellenkező oldalán van, mint a

k_{1}

kör

O_{1}

középpontja. ‐ Ha

C

k_{1}

körbe esik, akkor, mint láttuk,

γ = 90^{\circ} + δ

, tompa szög, így

α

és

β

hegyes szögek,

A

és

B

A_{1} B_{1}

-nek egy oldalán vannak, és ugyanezen az oldalon van

O_{1}

is, mint az

A B

szakasz felezőpontja. Az

A B B_{1} A_{1}

konvex négyszög átlóinak metszéspontjaként

C

is ugyanezen oldalán van

A_{1} B_{1}

-nek, ennélfogva az

A_{1}

B_{1}

C

-vel meghatározott

k_{1}

körnek az

A_{1} C B_{1}

szög szárai közé eső íve az ellenkező oldalon van. Ehhez az ívhez

O'

középpontjában

2 (90^{\circ} + δ) > 180^{\circ}

-os szög tartozik, ezért

O'

ugyancsak a

C

-vel ellentétes oldalon van, így

O'

, ill.

k'

valóban azonos

O_{3}

, ill.

k_{3}

-mal.
Ha

C

k_{1}

-en kívül van, akkor egyszersmind

A_{1} B_{1}

-nek

O_{1}

-gyel ellenkező oldalán van. Ugyanis ilyenkor

γ = 90^{\circ} - δ

, hegyesszög. Ha

α

és

β

is hegyesszögek, akkor

A

és

B

ismét

O_{1}

oldalán vannak, hegyesszögű háromszögben pedig

A_{1}

és

B_{1}

elválasztják

C

-t

B

, ill.

A

-tól. Ha pedig pl.

β

tompaszög, akkor

B

k_{1}

-nek rövidebb

A_{1} B_{1}

ívén van, az

A_{1} B_{1}

egyenesnek

O_{1}

-gyel ellenkező oldalán, mert

A_{1} B B_{1} ∢ = 180^{\circ} - δ > 90^{\circ}

C

pedig az

A_{1} B

szakasznak

B

-n túli meghosszabbításán. ‐ Ezek szerint

k'

-nek az

A_{1} C B_{1}

szög szárai közé eső,

2 (90^{\circ} - δ) < 180^{\circ}

-os középponti szöghöz tartozó íve az

O_{1}

oldalán van, ezért

O'

ismét az ellenkező oldalon van.

C

k_{3}

-nak bármely az

A_{1}

és

B_{1}

-től különböző pontja lehet, ugyanis így

A_{1}

és

B_{1}

-gyel együtt szintén egyértelműen meghatározza a háromszöget:

A

C B_{1} = b

egyenes és

C A_{1} = a

-ra az

A_{1}

-ben merőleges egyenes metszéspontja, és hasonlóan kapható

B

is. Viszont pl.

C \equiv A_{1}

feltevése a kizárt

A C B ∢ = 90^{\circ}

esetre vezet.
Eredményünk így is kimondható: ha egyenesszakasszá elfajult háromszöget nem fogadunk el, akkor

A

és

B

egyik mértani helye a

k_{1}

kör az

A_{1}

és

B_{1}^{*}

, ill.

B_{1}

és

A_{1}^{*}

pontok kivételével, és

C

mértani helye

k_{3}

A_{1}

és

B_{1}

pontok kivételével;

k_{1}

és

k_{3}

helyére

k_{2}

k_{4}

-et írva megállapításunk a másik mértani hely-párt adja, a ,,csillagos'' pontokat természetesen azokon véve.

Megjegyzések. 1. Akik ismerik a háromszög Feuerbach-körének alaptulajdonságait, azok számára nyilvánvaló, hogy

O_{3}

felezi a háromszög

C

-ből kiinduló magasságának

C

és az

M

magasságpont közti szakaszát, ennélfogva

O_{3} C

A

-nak bármely helyzetében merőleges

A B

-re. Ha tehát

A

(és vele

B

) a

k_{1}

-en egyenletesen forog, akkor ugyanez áll

C

-re is a

k_{3}

-on, és mindhárom csúcs egyszerre érkezik a kizárt pontokba.
2. A legtöbb dolgozat csak azt állapította meg, hogy

A

és

B

egy olyan köríven vannak, amelynek pontjaiból

A_{1} B_{1}

látószöge

δ

, de nem vették észre, hogy

A

és

B

e körnek mindig átellenes pontjai, továbbá, hogy az

A B C

háromszög tompaszögű is lehet.