| Feladat: | 495. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Bárczy Zsolt , Hild Erzsébet | ||
| Füzet: | 1959/február, 37 - 38. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Trigonometrikus egyenletek, Szögfüggvények, síkgeometriai számítások, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1958/április: 495. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: A feltevésnél fogva van olyan derékszögű háromszög, amelynek egyik hegyes szöge , ill. . 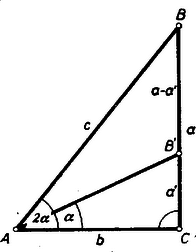 Ilyen az 1. ábrán , ill. , ezekben a , ill. szög melletti befogó közös és ettől indulva e szögek forgási értelme egyező, így felezi a szöget, ennélfogva a szögfelező által a szembenfekvő oldalon létesített részek arányára vonatkozó tétel szerint A bal oldali tört számlálóját és nevezőjét -vel, a jobb oldaliét pedig -vel osztva a hányadosokban a , ill. tangensét, ill. a koszinuszát a derékszögű háromszögben értelmező arányokra ismerünk rá, és így ezek beírásával éppen a bizonyítandó egyenlőséget kapjuk.
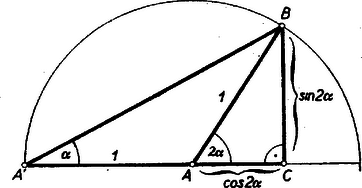 II. megoldás: A 2. ábrán az , ill. derékszögű háromszögekben a egyenlőséget a megrajzolt körbeli helyzet, az egyenlőség biztosítja, ezekben a , ill. -val szemben fekvő befogó közös, a másik befogó pedig , ill. . Ezekkel a bizonyítandó egyenlőség bal oldala számára mind , mind tangensét kifejezve hányadosukból átalakítással a kívánt jobb oldalt kapjuk:
|