Kezdőlap


Feladat:	494. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Balogh K. , Bárczy Zs. , Biborka T. , Bollobás B. , Bornes Klára , Czékus L. , Dudás J. , Fejes L. , Flanek L. , Fritz J. , Gáti P. , Gazsi L. , Gergely A. , Gy. Molnár Sz. , Hajna J. , Holop A. , Horváth Dénes , Horváth Tibor , Inotai A. , Jahn A. , Kárpáti A. , Kiss Ádám , Komlós J. , Krámli A. , Lengvári I. , Máté Zs. , Máthé Cs. , Mezey F. , Miklós A. , Molnár E. , Muszély Gy. , Müller Miksa , Nagy Márton , Nagy Péter , Nagymajtényi Emőke , Nováki A. , Pál G. , Parti Enikő , Posch Margit , Raisz Klára , Sáry Barna Sz. , Simai L. , Székely J. , Szűcs J. , Téry L. , Tihanyi A. , Tomcsányi Gy.
Füzet:	1959/január, 14 - 17. oldal		PDF \| MathML
Témakör(ök):	Párhuzamos szelők tétele, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/április: 494. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen $A M$ és $N D$ metszéspontja $F$ . Ekkor a feladathoz fűzött megjegyzés folytán ‐ a szakaszok irányítását is figyelembe véve ‐ az $F$ -nek akár az $A L$ szakaszon, akár azon kívüli helyzete esetén $A L = A F + F L$ , így a vizsgálandó osztóviszony:

\begin{matrix} \frac{A L}{L M} = \frac{A F}{L M} + \frac{F L}{L M} . \end{matrix}

(1)

A jobb oldal második tagjában álló osztóviszonyt ‐ amelynek szokásos rövid jele: (

F M L

)¹ ‐

D N

és

B C

párhuzamosságának felhasználásával előbb a vele egyenlő

(D E L)

, majd hasonlóan

N E ∥ A M

alapján a

(D N F)

, végül ismét

D N ∥ B C

alapján a

(B C M)

osztóviszonnyal helyettesíthetjük, ennek értéke pedig adatként használható:

\begin{matrix} (F M L) = \frac{F L}{L M} = \frac{D L}{L E} = \frac{D F}{F N} = \frac{B M}{M C} = (B C M) = m \end{matrix}

(2)

(bármelyik két egymás utáni ponthármas első, második, harmadik pontjai egymásnak megfelelői).

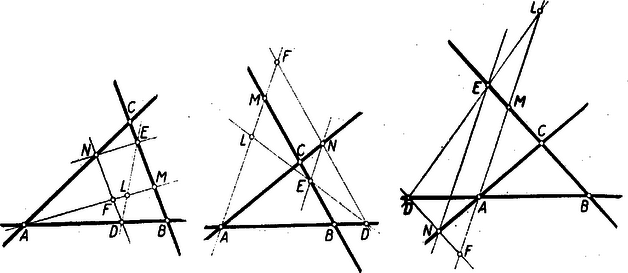Az első tagbeli hányados számlálójának és nevezőjének

F M

-mel való szorzása után az

(A M F) = (A C N) = n

osztóviszony (ismét

D N ∥ B C

alapján) és az

F M / L M

hányados szorzatával egyenlő, és itt az utóbbi tényező

F M = F L + L M

, valamint (2) alapján

m + 1

-gyel egyenlő:

\begin{matrix} \frac{A F}{L M} = \frac{A F}{F M} \cdot \frac{F M}{L M} = \frac{A N}{N C} \cdot \frac{F L + L M}{L M} = n (\frac{F L}{L M} + 1) = n (m + 1) . \end{matrix}

(3)

Most már (1)‐(3) szerint valóban áll a bizonyítandó egyenlőség:

\begin{matrix} \frac{A L}{L M} = n (m + 1) + m = m n + m + n . \end{matrix}

Müller Miksa (Makó, József A. g. II. o. t.)

II. megoldás: A bizonyítandó egyenlőség jobb oldalán az

(m + 1) (n + 1)

szorzat három tagját felismerve adjuk hozzá mindkét oldalhoz a hiányzó negyediket, az 1-et és igyekezzünk az

\frac{A L}{L M} + 1 = \frac{A L + L M}{L M} = \frac{A M}{L M}

hányadost az

m + 1 = \frac{B M}{M C} + 1 = \frac{B C}{M C}

és

n + 1 = \frac{A N}{N C} + 1 = \frac{A C}{N C}

hányadosok szorzataként előállítani. (Ezek egyébként az

\frac{A M}{L M} = - \frac{A M}{M L}

\frac{B C}{M C} = - \frac{B C}{C M}

és

\frac{A C}{N C} = - \frac{A C}{C N}

átalakítások szerint ugyancsak tekinthetők osztóviszonyoknak, csupán az a szokatlan, hogy így

- (A L M)

- (B M C)

és

- (A N C)

-ben a ,,későbben létrejött''

L

, ill.

M

, ill.

N

pont szerepel alappontként.) Valóban, az I. megoldásban használt vagy azokhoz hasonló átalakításokkal:

\begin{matrix} \frac{A M}{L M} = \frac{A F + F M}{L M} = \frac{\frac{A F}{F M} + 1}{\frac{L M}{F M}} = \frac{\frac{A N}{N C} + 1}{\frac{L M}{F L + L M}} = \\ = (n + 1) \cdot \frac{F L + L M}{L M} = (n + 1) (\frac{F L}{L M} + 1) = (n + 1) (m + 1) . \end{matrix}

Ezzel bizonyításunkat befejeztük.

Megjegyzések. 1. Mindkét megoldásban kissé felületesen jártunk el, nem voltunk tekintettel arra, hogy mindazok a hányadosok, pontok, amelyekről beszéltünk,

M

és

N

-nek bármely felvétele esetén léteznek-e, egyértelműen meg vannak-e határozva, továbbá hogy az alkalmazott átalakításokat szabad-e mindig végrehajtani. Most pótoljuk ezeket a hiányokat.
Igen egyszerű annak biztosítása, hogy az adott

m

és

n

osztóviszonyoknak (az osztásoknak) legyen értelmük: nem lehet

M C = N C = 0

, azaz

M

és

N

-et nem választhatjuk

C

-ben. Már hosszabb meggondolást igénylő kérdés, hogy a több lépéssel előálló

L

pont határozott-e. Ez csak akkor nem állna, ha az

A M

és

D E

egyenesek egybeesnének vagy párhuzamosak lennének.
Egybeesésük akkor és csak akkor következnék be, ha

A B

-vel való

A

, ill.

D

közös pontjuk is, és

B C

-vel való

M

, ill.

E

közös pontjuk is egybeesne. Már most

D

értelmezésénél fogva

D \equiv A

akkor és csak akkor áll be, ha

N \equiv A

; ilyenkor

E

értelmezésénél fogva

E \equiv M

is bekövetkezik, ennélfogva a

N \equiv A

, másképpen a

n = 0

esetet ugyancsak ki kell zárnunk. Fordítva,

E \equiv M

-ből ugyancsak következik

N \equiv A

; így ugyanis a

N E

és

A M

párhuzamosok egybeesnek, ennélfogva az

A C

-vel való egyetlen közös pontjuk:

N

, ill.

A

is egybeesnek (

A M

-nek

A C

-vel nem lehet egynél több közös pontja, mert

B C

-t az egymástól különböző

M

, ill.

C

pontban metszik.) Más szóval az

N \equiv A

egybeesésnek szükséges és elegendő feltétele az

E \equiv M

egybeesés.

D E

-nek

A M

-mel való párhuzamossága pedig

E

értelmezése révén azt jelentené, hogy

D E

egybeesik

N E

-vel, ennélfogva vagy

D \equiv N

(ekkor egybeesnek

A

-val, ezt az esetet már kizártuk), vagy

D N ∥ A M

. Ámde értelmezésnél fogva

D N ∥ B C

, ennélfogva ekkor

A M ∥ B C

, ami ellentétben áll

M

értelmezésével. Eszerint itt további esetet nem kell kizárnunk.
Hogy a vizsgálandó

A L ∥ L M

osztóviszonynak legyen értelme, nem vehetjük fel

M

N

-et úgy, hogy a megszerkesztett

L

egybeessék

M

-mel. Erre csak az

E \equiv M

egybeesés vezethetne, ezt már kizártuk.
Utolsó ilyen kérdésünk: szabad volt-e

F M

-mel hányadost ,,bővíteni, ill. egyszerűsíteni'', nem áll-e fenn az

F M = 0

,,veszélye''? ‐ Nem, mert

F

és

M

az egymással párhuzamos és

N ≢ C

folytán egymástól különböző

N D

, ill.

B C

egyenes egy‐egy pontja.
Ezek szerint a bebizonyított egyenlőség érvényes, ha

M

nem esik

C

-be és

N

nem esik sem

C

-be, sem

A

-ba.
2. Könnyű belátni, hagy az ezek után ugyancsak ,,veszélyesnek'' gondolható

M \equiv B

egybeesést nem kell kizárni. Ezzel

N

-nek bármely megengedett helyzetében

L \equiv D

és egyenlőségünk bal oldala

\begin{matrix} \frac{A L}{L M} = \frac{A D}{D B} = \frac{A N}{N B} = n \end{matrix}

és ez egyezik a jobb oldalnak

m = 0

-val adódó értékével.

3. Ábráink csupán

M

és

N

felvételében különböznek, tulajdonképpen egy is elég volna, vagy még egyre sincs szükség. A szakaszok irányítása nem nehezítette, hanem éppen könnyítette, egységessé tette a sokféle lehetőség vizsgálatát. Mégis ajánljuk olvasóinknak, hogy még több ábrán kövessék az adott gondolatmenetet.

M

és

N

mindegyike számára már ez is három lehetőség: az oldal szakaszon (itt

m

n > 0

), vagy a meghosszabbítások valamelyikén (itt

- 1 < m

n < 0

, ill.

m

n < - 1

); további finomítás: az oldalszakasz felezőpontjában, ill. első vagy második felében (

m

n = 1

, ill.

< 1

, ill.

> 1

¹Lásd pl. Kárteszi Ferenc: A Menelaos- és a Ceva-féle tétel. KML. XI. kötet 67‐75. o., 1955. november.