Feladat:	485. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Biborka T. ,  Biró G. ,  Bleyer A. ,  Bollobás B. ,  Bornes Klára ,  Budai M. ,  Budai Zsuzsanna ,  Bürger N. ,  Csikor F. ,  Czékus L. ,  Doromby Annamária ,  Dömötör Gy. ,  Fejes L. ,  Fekete J. ,  Flanek L. ,  Fritz J. ,  Grüner Gy. ,  Hansághy T. ,  Horváth Z. ,  Jahn A. ,  Kátai Sz. ,  Kovács B. ,  Krámli A. ,  Kugler Emese ,  Máté Zs. ,  Máthé Cs. ,  Mezey F. ,  Muszély Gy. ,  Müller M. ,  Nováky A. ,  Pál G. ,  Posch Margit ,  Raisz Klára ,  Reischl T. ,  Rohrböck Krisztina ,  Sylvester Á. ,  Szőke A. ,  Szőllős T. ,  Tanner Éva ,  Tihanyi A. ,  Timár P. ,  Zánkai D.
Füzet:	1959/április, 97 - 100. oldal		PDF  |  MathML
Témakör(ök):	Eltolás, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/március: 485. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.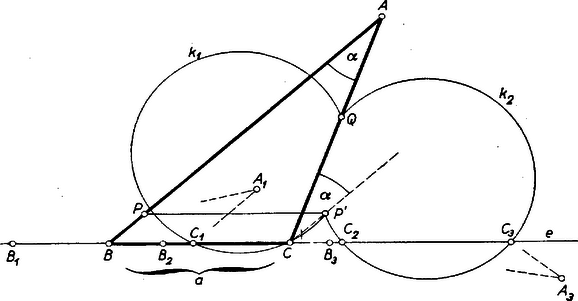   1. ábra   I. megoldás: Legyenek az adott egyenes és a pontok $e$, $P$, $Q$. Ezek a keresett $ABC$ háromszöggel szemben négy elhelyezési követelményt támasztanak: $B$ és $C$-nek $e$-re, $AB$ és $AC$-nek $P$, ill. $Q$-ra kell illeszkednie. Ezek a követelmények egyrészt pótolják azt a hiányt, hogy a szükséges három (független) alkotórésszel szemben itt csak kettő van előírva, másrészt a háromszög helyzetét is meghatározzák. Tegyük fel egyelőre, hogy $P$ és $Q$ az $e$-nek ugyanazon partján van. Képzeljük a feladatot megoldottnak, és legyen egy a követelményeknek megfelelő háromszög $ABC$, amelyben $BC=a$, $BAC\sphericalangle =\alpha$ (1. ábra). Hogy a méret- és helyzetkövetelményeket kapcsolatba hozzuk, toljuk el a $BC$ szakasz $B$ végpontját $P$-be, és legyen ekkor $C$ új helyzete $P\text{'}$, vagyis $PP\text{'}\parallel e$ és $PP\text{'}=a$. A $PBCP\text{'}$ négyszög paralelogramma, ezért $CP\text{'}\parallel BP$, és így az $AB$ és $AC$, másképpen a $BP$ és $CQ$ egyenesek közti a szög $C$-ben is előállt $CP\text{'}$ és $CQ$ között. Ennélfogva a $P\text{'}Q$ szakaszt $C$-ből $\alpha$ szög alatt látjuk. Ezek alapján a szerkesztés a következő: a $P$-n át $e$-vel párhuzamosan húzott $e_1$-re $P$-től felmérjük az $a$ szakaszt, és megszerkesztjük azt a $k_1$, $k_2$ körív-párt, amelynek pontjaiból $P\text{'}Q$ látószöge $\alpha$. $k_1$, $k_2$-nek minden az $e$-vel közös pontja egy megoldást ad $C$-re, ebből a $CP\text{'}PB$ paralelogramma negyedik csúcsaként kapjuk meg $B$-t, végül $CQ$ és $BP$ metszéspontjaként $A$-t. Valóban, így $AB$ és $AC$ átmegy $P$-n, ill. $Q$-n, $BC=PP\text{'}=a$, és $BAC\sphericalangle =\alpha$, mert $AB\parallel CP$, és így $BAC\sphericalangle =P\text{'}CQ\sphericalangle =\alpha$, mert váltószögek. Az 1. ábrán a $k_1$, $k_2$ ívpárnak $e$-vel $4$ közös pontja van: $C$, $C_1$, $C_2$, $C_3$. Az utóbbi kettő az $e$-nek $P$, $Q$-val ellentett partján fekvő $ABC$ háromszöget ad: 1. $P$-n és $Q$-n e háromszögek megfelelő oldalszakasza nem megy át, csak az oldalegyenes. Hasonlóan a $C_1$-gyel adódó $A_1{B}_1{C}_1$ háromszögnek $A_1{B}_1$ oldala átmegy $P$-n, $A_1{C}_1$-nek viszont csak a meghosszabbítása megy át $Q$-n. Csak ilyen megoldás várható akkor is, ha $P$ és $Q$ az $e$-nek ellentétes partjain feküsznek. Hogy $A_3{B}_3{C}_3$ (és hasonlóan $A_2{B}_2{C}_2$) is megfelelő megoldás, ennek bizonyítása csak a szögek közti egyenlőség indokolásában tér el a fentitől: ezek most egyállású szögek. 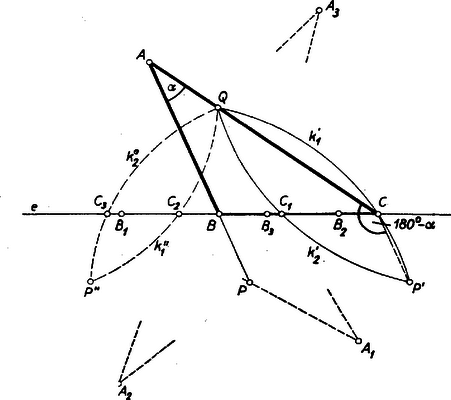    2. ábra   Megvizsgáljuk azt a helyzetet is, ha $e$ szétválasztja a $P$, $Q$ pontokat (2. ábra). Előbbi elemzésünk csak annyiban módosul, hogy $P\text{'}Q$-t $C$-ből nem $\alpha$, hanem ${180}^{\circ }-\alpha$ szög alatt látjuk, a szerkesztésben $k_1$, $k_2$-n az ennek megfelelő látószög-körívpár értendő. Az így szerkesztett $ABC$ háromszögekben a $CP\text{'}$ és $CQ$ félegyenesek egyike megegyező, másika ellentett irányú az $AB$, ill. $AC$ félegyenessel, ennélfogva $BAC\sphericalangle ={180}^{\circ }-P\text{'}CQ\sphericalangle =\alpha$. A $k_1$, $k_2$ körív-pár és $e$ közös pontjainak száma legfeljebb $4$. Másrészt $P\text{'}$ szerkesztésére, $P$-nek $a$-val való eltolására $e$ irányában, két lehetőség van (a 2. ábrán $P\text{'}\text{'}$, a $P\text{'}\text{'}$-ből előállított $B_3{C}_3$ szakasz betűzési iránya ezért ellentett $BC$-ével), így a megoldások száma legfeljebb $8$. (De lehet, hogy egy megoldás sincs.) Ha $e$ szétválasztja $P$-t és $Q$-t, akkor a $P\text{'}$ és $P\text{'}\text{'}$-höz tartozó ívpárok mindegyikének pontosan egy pontja van $e$-n, ilyenkor a megoldások száma pontosan $4$. Ha $P\text{'}$ egybeesik $Q$-val, akkor a fenti eljárás nem használható, a körívek ponttá zsugorodnak össze. Ilyenkor csak a $P\text{'}$ révén adódó megoldásokról lehet szó. Ha a pontok egyike, pl. $P$ az $e$-n van, akkor ez a $B$ csúcs, a $P\text{'}$ megadja $C$-t, $Q$-t pedig $CQ$-ból a vele $\alpha$ szöget bezáró két iránnyal $B$-n át húzott párhuzamosok metszhetik ki; azonban megvizsgálandó, hogy az $A$-nál létrejött ‐ belső és külső ‐ szögek közül valóban a belső egyenlő-e $\alpha$-val. ‐ Ha végül $P$ és $Q$ mindegyike $e$-n van, akkor $PQ=a$ esetén végtelen sok megoldás van, $PQ\ne a$ esetén pedig nincs megoldás.   Megjegyzések. 1. A helyzeti és méretadatokat néhány dolgozat a $PQ$ szakasznak $BQ\text{'}$-be való eltolása útján hozta kapcsolatba (3. ábra). 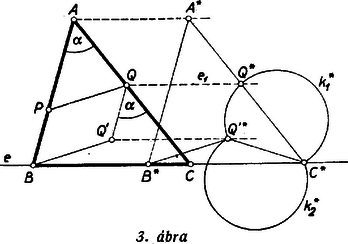    3. ábra   Ekkor $CQ\text{'}$-t $Q$-ból $\alpha$, ill. ${180}^{\circ }-\alpha$ szögben látjuk. Bár így az adott helyzetű szakaszt ismeretlen helyzetbe toltuk át, némi többletmunkával megoldáshoz juthatunk a fentivel lényegében azonos gondolatmenettel. Ugyanis $e$-nek tetszés szerinti $B^{*}$ pontjából, mint $B$-nek eltolt megfelelőjéből kiindulva megszerkeszthetjük ábránknak egy az $e$ mentén eltolt megfelelőjét, majd ezt a ,,csillagos'' alakzatot $Q^{*}$-nál fogva $Q$-ba ,,visszatolva'' megkapjuk a megoldást. Az ábrán $e_1$, $C$, $Q\text{'}$ alkalmas középpontra nézve tükrös párja az előbbi $e$, $Q$, $P\text{'}$-nek. 2. Az 1. ábrán vázolt három megoldás nem egybevágó; a helyzetkövetelmények e tekintetben természetesen nem pótolják a hiányzó méret-adatot. 3. A legtöbb dolgozat szerint a megoldások száma legfeljebb $2$, ritkán $4$. A hiány persze nem azon múlik, hogy az adott pontpár minden ábrában $e$-nek ugyanegy oldalán van ‐ bár a másik lehetőséget csak szórványosan említik ‐, hiszen ilyenkor csak $4$ megoldás van. Hanem azon, hogy legtöbben a $k_1$, $k_2$ ívekből és $P\text{'}$ két lehetséges helyzetéből csak egyet-egyet vesznek figyelembe. ‐ Egy dolgozat szerint $P$ és $Q$ közül az ,,$e$-hez közelebbin'' át húzott párhuzamosra a ,,másik pont felé'' mérjük fel $a$-t. Egy másik $C$-t $Q$-ba tolva ,,az előbbi megoldás szimmetrikusát'' kapja. Néhányan kizárják a $PQ\parallel e$ és a $PQ\perp e$ lehetőségeket, ami hiba ugyan, mégis némi körültekintésre mutat. Van, aki szerint $a<PQ$ esetén nincs megoldás. Mindezek (és más hibák) szerint igen elterjedt az a többnyire nem is tudatos felfogás, hogy egy ábráról mindent le lehet olvasni. Persze az a felfogás is lehet túlzás, hogy több ábrát rajzoljunk, mert egyetlen ábra néha inkább félrevezet, mint tájékoztat. Olyankor azonban mindenesetre célszerű több különböző felvételből kiindulva végigjárni a meggondolást, ha ‐ mint itt is ‐ nemcsak alakról van szó, hanem helyzetről is. Az alábbiakban ‐ helyszűke miatt ‐ egy más megoldás alapgondolatát mi is egyetlen ábrához kapcsolódva vázoljuk, ezt azonban tudatosan tesszük, és az összes megoldások megkeresését, valamint a diszkussziót az olvasóra bízzuk. II. megoldás (vázlat): Keressük $A$ helyzetét a mértani helyek módszerével. Az $A$ csúcs azon két (teljes) kör egyikén van, amelynek pontjaiból $PQ$-t $\alpha$, vagy ${180}^{\circ }-\alpha$ szög alatt látjuk ($\alpha$ a látószög egyrészt olyankor, ha $A$ a $BP$ és $CQ$ félegyenesek mindegyikén rajta van, másrészt olyankor, ha $A$ egyiken sincs rajta ; különben ${180}^{\circ }-\alpha$ a látószög). Az egyik ilyen $k_1$ kör sugara legyen $r_1$, középpontja a 4. ábrán $O_1$. ─ Tekintsük másrészt az $ABC$ háromszög $k_2$ körülírt körét, ennek középpontja $O_2$; $k_2$-nek $r_2$ sugarát és $O_2$-nek $e$-től mért $d$ távolságát $a$ és $\alpha$-ból megszerkeszthetjük. 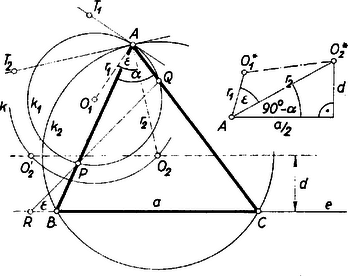    4. ábra   $k_2$ helyzetének megállapítása céljára megmutatjuk, hogy az $A{O}_1$ és $A{O}_2$ sugarak $ϵ$ szöge egyenlő az $e$ és $PQ$ egyenesek $R$ közös pontjánál keletkező szögek egyikével. Legyen $T_1$ a $k_1$-hez $A$-ban húzott érintőnek egy olyan pontja, amely $AP$-nek a $Q$-val ellentett partján van, és $T_2$ a $k_2$-höz $A$-ban húzott érintőnek $Q$-tól $AB$ által elválasztott pontja. Ekkor $T_{1}AP\sphericalangle =AQP\sphericalangle =QCR\sphericalangle +QRC\sphericalangle$, $T_{2}AP\sphericalangle =T_{2}AB\sphericalangle =ABC\sphericalangle =QCR\sphericalangle$, ezekkel valóban $ϵ=O_{1}A{O}_2\sphericalangle =T_{1}A{T}_2\sphericalangle =T_{1}AP\sphericalangle -T_{2}AP\sphericalangle =QRC\sphericalangle$. Most már $r_1$, $r_2$, és $ϵ$-ból megszerkeszthetjük az $O_{1}A{O}_2$ háromszög alakját. Az így megkapott $O_1{O}_2$-vel $O_1$ körül $k$ kört írva egy mértani helyet kapunk $O_2$-re, egy másik ilyet pedig az $e$-től $d$ távolságban húzott párhuzamos ad. $O_2$ ismeretében elhelyezhetjük $k_2$-t, ennek $k_1$-gyel közös pontjaként megkapjuk $A$-t, majd $AP$ és $AQ$ révén $B$ és $C$-t. 1Az ábra eddigi részleteinek áttekinthetősége érdekében az $A_3{B}_3{C}_3$ háromszögnek $A_3$-ba befutó oldalai csonkán vannak feltüntetve, ugyanígy $A_1$-nél is ; a távol eső $A_2$-t pedig nem tüntettük fel.