Kezdőlap


Feladat:	464. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Németh Márta , Székely Jenő , Tihanyi Ambrus
Füzet:	1958/október, 46 - 48. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Tengelyes tükrözés, Derékszögű háromszögek geometriája, Szögfelező egyenes, Beírt kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1958/január: 464. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Az $A B C$ derékszögű háromszög $A$ és $B$ csúcsának szögfelezőire tükrözzük a derékszögű csúcsot (1. ábra), jelöljük az így kapott pontokat $C_{1}$ -gyel és $C_{2}$ -vel, a szögfelezők metszéspontjait a befogókkal 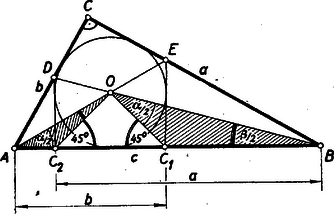$D$ -vel és $E$ -vel.

1. ábra

A tükrözés miatt

D C_{2}

és

E C_{1}

érintői lesznek az

O

középpontú beírt körnek s mivel mindkettő merőleges a

c

átfogóra, párhuzamos érintők lesznek. Így távolságuk

\begin{matrix} C_{1} C_{2} = 2 ϱ \end{matrix}

(

ϱ

jelöli a beírt kör sugarát).
Az

O C_{1} C_{2}

derékszögű egyenlő szárú háromszög befogói Pythagoras-tétellel kiszámíthatók:

\begin{matrix} O C_{1} = O C_{2} = ϱ \sqrt[]{2} . \end{matrix}

(1)

A tükrözés következtében:

\begin{matrix} B C_{2} = a és A C_{1} = b, \end{matrix}

ezért

\begin{matrix} A C_{2} = c - a és B C_{1} = c - b . \end{matrix}

(2)

O C_{1} C_{2}

háromszög derékszögű és egyenlő szárú,

C_{1}

-nél és

C_{2}

-nél levő szögei

45^{\circ}

-osak. Az

O A C_{2}

háromszögnek a

C_{2}

-nél levő

45^{\circ}

-os szög külső szöge, az

\frac{α}{2}

szöget tehát a háromszög

O

-nál levő szöge

45^{\circ}

-ra egészíti ki; így ez a szög csak

\frac{β}{2}

lehet (hiszen az eredeti derékszögű háromszögben

\frac{α}{2} + \frac{β}{2} = 45^{\circ}

). Ugyanígy a

B O C_{1}

háromszög

O

-nál levő szöge

\frac{α}{2}

. A két háromszög tehát hasonló egymáshoz, megfelelő oldalaik aránya megegyezik:

\begin{matrix} A C_{2} : C_{2} O = O C_{1} : C_{1} B . \end{matrix}

Az aránypárba az (1) és (2) alatti értékeket beírva:

\begin{matrix} (c - a) : ϱ \sqrt[]{2} = ϱ \sqrt[]{2} : (c - b), \end{matrix}

azaz

\begin{matrix} 2 ϱ^{2} = (c - a) (c - b) . \end{matrix}

2-vel megszorozva mindkét oldalt:

\begin{matrix} {(2 ϱ)}^{2} = 2 (c - a) (c - b) . \end{matrix}

Ezzel épp a bizonyítandó tételt igazoltuk.

Székely Jenő (Pécs, Nagy Lajos g. I. o. t.)

II. megoldás: Ismeretes, hogy a háromszög területe a beleírható kör sugarával és a félkerülettel kifejezhető:

\begin{matrix} t = ϱ s = ϱ \frac{a + b + c}{2} . \end{matrix}

Derékszögű háromszög esetén:

\begin{matrix} t = \frac{a b}{2} . \end{matrix}

A kettőt összevetve

\begin{matrix} 2 ϱ = \frac{2 a b}{a + b + c} . \end{matrix}

Emeljük négyzetre mindkét oldalt:

\begin{matrix} 4 ϱ^{2} = \frac{4 a^{2} b^{2}}{a^{2} + b^{2} + c^{2} + 2 a b + 2 a c + 2 b c} . \end{matrix}

A Pythagoras-tétel alkalmazásával:

\begin{matrix} 4 ϱ^{2} = \frac{4 (c^{2} - b^{2}) (c^{2} - a^{2})}{c^{2} + c^{2} + 2 a b + 2 a c + 2 b c} = \frac{4 (c - b) (c + b) (c - a) (c + a)}{2 [c (a + c) + b (a + c)]} = \\ = \frac{2 (c - b) (c + b) (c - a) (c + a)}{(c + b) (a + c)} = 2 (c - a) (c - b) . \end{matrix}

Tihanyi Ambrus (Bp., V., Apáczai Csere g. II. o. t.)

III. megoldás: Rajzoljuk meg az

a

b

c

oldalú derékszögű háromszögbe a

ϱ

sugarú beírható kört és rajta az érintési pontokat (2. ábra).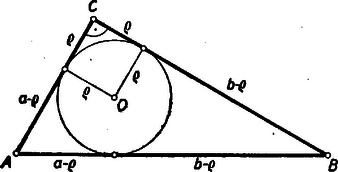

2. ábra

Egy pontból a körhöz húzható érintőszakaszok egyenlősége alapján könnyen látható, hogy a

c

átfogó a következő két szakasz összege:

\begin{matrix} c = (a - ϱ) + (b - ϱ) . \end{matrix}

Innen

\begin{matrix} 2 ϱ = a + b - c, \end{matrix}

négyzetre emelve s a Pythagoras-tételt fölhasználva:

\begin{matrix} 4 ϱ^{2} = a^{2} + b^{2} + c^{2} + 2 a b - 2 a c - 2 b c = 2 c^{2} + 2 a b - 2 a c - 2 b c = \\ = 2 c (c - a) - 2 b (c - a) = 2 (c - a) (c - b) . \end{matrix}

Állításunkat ezzel bizonyítottuk.

Németh Márta (Kazincbarcika, Vegyip. tech. I. o. t.)