Kezdőlap


Feladat:	462. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Gáspár Mária , Náray Szabó Gábor
Füzet:	1958/szeptember, 22 - 24. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/december: 462. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az 1. ábrán megrajzoltunk az $O$ középpontú körben egy $P$ ponton átmenő két egymásra merőleges $h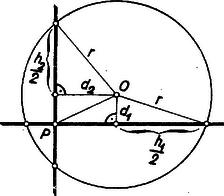_{1}$ , $h_{2}$ húrt.

1. ábra

Jelöljük a húroknak a középponttól mért merőleges távolságát

d_{1}

-gyel és

d_{2}

-vel, a kör sugarát

r

-rel. A

d_{1}

és

d_{2}

meghúzásával keletkező derékszögű háromszögekre a Pythagoras-tételt felírva:

\begin{matrix} {(\frac{h_{1}}{2})}^{2} = r^{2} - d_{1}^{2} azaz h_{1}^{2} = 4 r^{2} - 4 d_{1}^{2}, \\ {(\frac{h_{2}}{2})}^{2} = r^{2} - d_{2}^{2} azaz h_{2}^{2} = 4 r^{2} - 4 d_{2}^{2} . \end{matrix}

Így a húrok négyzeteinek összege:

\begin{matrix} h_{1}^{2} + h_{2}^{2} = 8 r^{2} - 4 (d_{1}^{2} + d_{2}^{2}) . \end{matrix}

d_{1}^{2} + d_{2}^{2}

viszont a

d_{1}

és

d_{2}

oldalú téglalap átlójának négyzetével egyenlő, az átló pedig az

O

középpont és a fix

P

pont távolsága. Így a húrok négyzetösszege valóban a

\begin{matrix} 8 r^{2} - 4 O P^{2} \end{matrix}

állandó értékkel egyenlő, a húrok helyzetétől függetlenül.
Ha az egyik húrt a kör átmérőjének vesszük fel, csak egy derékszögű háromszög keletkezik, és a téglalap egy szakasszá fajul. A levezetés és a tétel viszont érvényes marad ez esetben is, mivel a középponton átmenő húrnak a középponttól való távolsága 0. ‐ Ha

P

a kör középpontjával esik egybe, állításunk magától értetődő.

Gáspár Mária (Balassagyarmat, Balassa g. I. o. t.)

Megjegyzések: 1. Síkbeli tételünk igaz körön kívül fekvő

P

pontra is, ha belőle a körhöz két, egymásra merőleges szelőt húzhatunk.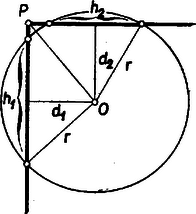

2. ábra

Ha az így húzható szelők a körből

h_{1}

és

h_{2}

húrt metszenek ki, itt is (l. a 2. ábrát):

\begin{matrix} {(\frac{h_{1}}{2})}^{2} = r^{2} - d_{1}^{2}, \\ {(\frac{h_{2}}{2})}^{2} = r^{2} - d_{2}^{2}, \end{matrix}

a két egyenlőség összeadásával

\begin{matrix} h_{1}^{2} + h_{2}^{2} = 8 r^{2} - 4 (d_{1}^{2} + d_{2}^{2}) . \end{matrix}

Mivel

d_{1}^{2} + d_{2}^{2} = O P^{2}

állandó, állításunkat igazoltuk.
Ha a

P

pont olyan távol van a körtől, hogy

P

-ből a körhöz már csak két merőleges érintőt húzhatunk, akkor

\begin{matrix} O P = r \sqrt[]{2} . \end{matrix}

Annak feltétele tehát, hogy a körhöz két egymásra merőleges szelőt húzhassunk, az, hogy

\begin{matrix} O P < r \sqrt[]{2} . \end{matrix}

2. Felvetődik a kérdés, igaz-e ilyen értelmű megállapítás a kör térbeli megfelelő alakzatának, a gömbnek húrjaira is? A válasz: igen, egy gömb belsejében levő ponton áthaladó három, egymásra páronként merőleges gömbi húr négyzetösszege állandó.
Jelöljük a húrok síkjai által kimetszett gömbi körök sugarait

ϱ_{1}

ϱ_{2}

ϱ_{3}

-mal, a gömb sugarát

R

-rel, a húrok hosszát

h_{1}

h_{2}

és

h_{3}

-mal, a gömbi körök síkjának távolságát a gömb középpontjától

d_{1}

d_{2}

d_{3}

-mal, az

O P

szakasz hosszát

d

-vel (3. ábr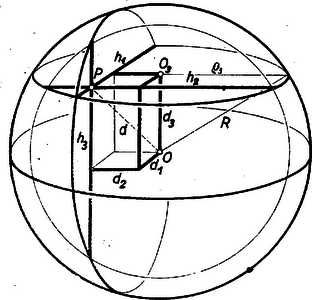a).

3. ábra

Az előző megoldás szerint:

\begin{matrix} h_{1}^{2} + h_{2}^{2} = 4 (2 ϱ_{3}^{2} - O_{3} P^{2}) . \end{matrix}

Pythagoras-tétele szerint

ϱ_{3}^{2} = R^{2} - d_{3}^{2} és O_{3} P^{2} = d^{2} - d_{3}^{2} .

Tehát

h_{1}^{2} + h_{2}^{2} = 8 R^{2} - 4 (d^{2} + d_{3}^{2}),

ugyanígy

\begin{matrix} h_{2}^{2} + h_{3}^{2} = 8 R^{2} - 4 (d^{2} + d_{1}^{2}) és h_{3}^{2} + h_{1}^{2} = 8 R^{2} - 4 (d^{2} - d_{2}^{2}) . \end{matrix}

Ebből

2 (h_{1}^{2} + h_{2}^{2} + h_{3}^{2}) = 24 R^{2} - 12 d^{2} - 4 (d_{1}^{2} + d_{2}^{2} + d_{3}^{2}) .

d_{1}

d_{2}

d_{3}

a 3. ábrán látható téglatest élei. A térbeli Pythagoras-tétel alapján:

\begin{matrix} d_{1}^{2} + d_{2}^{2} + d_{2}^{3} = d^{2}, \end{matrix}

azaz

\begin{matrix} h_{1}^{2} + h_{2}^{2} + h_{3}^{2} = 12 R^{2} - 8 d^{2} = 4 (3 R^{2} - 2 d^{2}), \end{matrix}

ami valóban állandó.

Náray Szabó Gábor (Bp. XI., József A. gimn. I. o. t.)

‐ Hasonlóan igazolhatjuk, hogy a gömbre általánosított tétel érvényes olyan kívüle fekvő pontokra is, melyekből a gömbhöz 3 egymásra merőleges szelő hozható.