Kezdőlap


Feladat:	437. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Fekete Jenő
Füzet:	1958/március, 79 - 80. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/szeptember: 437. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ábrán megrajzoltuk az $A B C$ derékszögű háromszöget a derékszögű csúcsból húzott $C M$ magassággal és a hegyesszögek szögfelezőivel.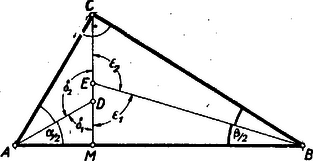

A feladatban megadott

13 : 17

arány egyaránt vonatkozhat a keletkező szögek közül

δ_{1}

és

ε_{1}

-re,

δ_{2}

és

ε_{2}

-re,

δ_{1}

és

ε_{2}

-re,

δ_{2}

és

ε_{1}

-re.
a) Nézzük azt az esetet, amikor

δ_{1} : ε_{1} = 13 : 17

. (Feltehetjük, hogy

δ_{1} < ε_{1}

, mert a fordított egyenlőtlenségnek a háromszögben a két hegyesszög felcserélése felel meg és ez nem vezet újabb háromszöghöz.)
A keletkezett

A M D

és

B M E

derékszögű háromszögekben

δ_{1}

\frac{α}{2}

szöget,

ε_{1}

pedig

\frac{β}{2}

-et egészíti ki derékszögre. Így

\begin{matrix} δ_{1} + ε_{1} = 2 \cdot 90^{\circ} - \frac{α}{2} - \frac{β}{2} = 135^{\circ} \end{matrix}

(mivel

α + β = 90^{\circ}

). Ezt kell felosztani

13 : 17

arányban.

30

egyenlő részre szétosztva

δ_{1}

-re

\frac{135}{30} \cdot 13 = 58, 5^{\circ}

jut. Így

\begin{matrix} \frac{α}{2} = 90^{\circ} - δ_{1} = 31, 5^{\circ}, \end{matrix}

vagyis

\begin{matrix} α = 63^{\circ}, s akkor β = 27^{\circ} . \end{matrix}

b) Vonatkoztassuk a megadott arányt

ε_{2}

-re és

δ_{2}

-re. Ezek a szögek

ε_{1}

-et, illetőleg

δ_{1}

-et

180^{\circ}

-ra egészítik ki, s így összegük

\begin{matrix} 2 \cdot 180^{\circ} - δ_{1} - ε_{1} = 225^{\circ}, \end{matrix}

Ebből az előbbi gondolatmenet szerint haladva

α = 75^{\circ}, β = 15^{\circ}

adódik.
c) Nézzük azt az esetet, amikor

δ_{1} : ε_{2} = 13 : 17

(az első szög hegyes, a második tompa). Ekkor a két szög különbsége

\begin{matrix} 90^{\circ} + \frac{β}{2} - (90^{\circ} - \frac{α}{2}) = \frac{α + β}{2} = 45^{\circ} . \end{matrix}

45^{\circ}

-ot tehát

17 - 13 = 4

részre kell osztanunk, ilyen egységből

δ_{1}

-re jut

13

, de akkor

δ_{1} = \frac{45^{\circ} \cdot 13}{4} > 90^{\circ}

. Ez pedig lehetetlen, hiszen

δ_{1}

hegyesszög. A

δ_{1}

és

ε_{2}

szögekre az arány tehát nem vonatkozhat, s ugyanúgy a

δ_{2}

és

ε_{1}

szögekre sem.

Fekete Jenő (Mosonmagyaróvár, Kossuth g. I. o. t.)

Megjegyzés: A feladat ugyanezzel a gondolatmenettel oldható meg, ha a szóbanforgó szögek aránya más megadott érték.