Kezdőlap


Feladat:	430. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bartha László , Füle Károly , Katona Gyula
Füzet:	1958/március, 74 - 75. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/május: 430. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A derékszögű háromszög (1. ábra) területe: $t = \frac{a b}{2}$ . Fejezzük ki a befogókat $c$ -vel és $α$ -val: $a = c sin α, b = c cos α$ , s használjuk fel a $sin 2 α = 2 sin α c o s α$ összefüggést: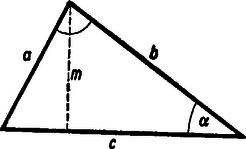

\begin{matrix} t = \frac{c^{2} sin α cos α}{2} = \frac{c^{2} sin 2 α}{4} \end{matrix}

1. ábra

Ezzel a feladat állítását igazoltuk.
‐ Ugyanígy célhoz jutunk, ha a

t = \frac{c m}{2}

területképletben az

m

magasságot

b

-vel és

α

-val, a

b

-t pedig

c

-vel és

α

-val fejezzük ki.

Füle Károly (Bp. V., Apáczai Csere g. II. o. t.)

II. megoldás: Tükrözzük a háromszöget a

b

befogóra (2. ábra).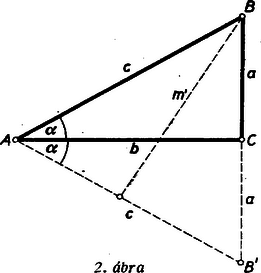

Így

\begin{matrix} t_{A B C ▵} = \frac{1}{2} t_{A B B' ▵} = \frac{1}{2} \frac{c m'}{2} = \frac{c^{2} sin 2 α}{4} \end{matrix}

mivel

m' = c sin 2 α

.
Ezzel ismét igazoltuk a bizonyítandó összefüggést.

Katona Gyula (Bp. VIII., Kandó híradásip. t. II. o. t.)

III. megoldás: Rajzoljuk meg a háromszög köré írt kört. A 3. ábráról leolvasható, hogy a kerületi és középponti szögek közti összefüggés alapján

B O C ∢ = 2 α

, továbbá a

B O C

háromszög területe fele az

A B C

háromszög területének, hiszen

C

-ből húzott magasságuk egyenlő, alapjuk pedig

\frac{c}{2}

, illetőleg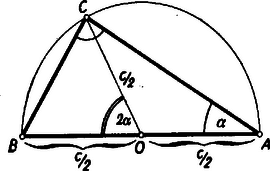

c

3. ábra

Ezért

\begin{matrix} t_{A B C ▵} = 2 t_{B O C ▵} = 2 {(\frac{c}{2})}^{2} \frac{sin 2 α}{2} = \frac{c^{2} sin 2 α}{4} \end{matrix}

Bartha László (Balassagyarmat, Balassa g. II. o. t.)