Kezdőlap


Feladat:	429. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balázs J. , Bartha L. , Bayer Magda , Bognár L. , Börzsöny László , Csanak Gy. , Csernyánszky Mária , Elbert Á. , Endrődy T. , Fejes L. , Füle K. , Gaál S. , Garamszegi P. , Gyene A. , Hajna J. , Hornyánszky T. , Kalász Klára , Katona Gy. , Kisvölcsey J. , Kolonits F. , Koszterszitz Gy. , Lefkovitsch S. , Losonczy L. , Madarász Klára , Magos A. , Máthé Cs. , Mayer G. , Mihályffy L. , Mocskónyi M. , Molnár Márta , Muszély Gy. , Náray Miklós (Bp.) , Náray Miklós (Győr) , Papp Éva , Raisz Klára , Rátkay Zs. , S. Nagy Erzsébet , Simonfai L. , Soós S. , Szász D. , Szatmári A. , Szatmári G. , Tamás Gy. (Bp.) , Tamás Gy. (Ózd) , Tápai A. , Tatai P. , Thaisz K. , Visy G.
Füzet:	1958/március, 72 - 74. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletek, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/május: 429. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Keressünk összefüggést az ismeretlen két oldal és a terület közt. Az $\frac{a b c}{4 t} = r$ és $t = ϱ s$ képletek felhasználásával

\begin{matrix} b c = \frac{10 t}{3} \end{matrix}

(1)

és

\begin{matrix} t = 2 s = 6 + b + c, \end{matrix}

amiből

\begin{matrix} b + c = t - 6. \end{matrix}

(2)

A Heron-képlet szerint, mivel

s = \frac{t}{2}

\begin{matrix} t = \sqrt[]{\frac{t}{2} (\frac{t}{2} - 6) (\frac{t}{2} - b) (\frac{t}{2} - c)}, \end{matrix}

azaz

\begin{matrix} t^{2} = \frac{t}{2} (\frac{t}{2} - 6) [\frac{t^{2}}{4} - \frac{t}{2} (b + c) + b c] . \end{matrix}

Felhasználva (1)-et és (2)-t, és

t^{2}

-tel osztva

\begin{matrix} 1 = \frac{1}{t} \frac{1}{2} (\frac{t}{2} - 6) [\frac{t^{2}}{4} - \frac{t}{2} (t - 6) + \frac{10 t}{3}] = \frac{1}{2} (\frac{t}{2} - 6) (\frac{t}{4} - \frac{t - 6}{2} + \frac{10}{3}) . \end{matrix}

A törtek eltávolítása és a zárójelek felbontása után ebből

t

-re a következő másodfokú egyenletet. kapjuk:

\begin{matrix} 3 t^{2} - 112 t + 960 = 0. \end{matrix}

Ennek gyökei

t_{1} = 24, t_{2} = \frac{40}{3} .

t

értéke 24, akkor (1) és (2) szerint

\begin{matrix} b c = 80, b + c = 18. \end{matrix}

Ebben az esetben tehát

b

és

c

a következő másodfokú egyenlet két gyökeként határozható meg:

\begin{matrix} x^{2} - 18 x + 80 = 0. \end{matrix}

Ebből a két oldal hossza

8

és

10

cm.
Ha

t = \frac{40}{3}

, akkor (1) és (2) szerint:

\begin{matrix} b c = \frac{400}{9} és b + c = \frac{22}{3} = \frac{66}{9} . \end{matrix}

b

és

c

a következő másodfokú egyenletnek tesznek eleget:

\begin{matrix} 9 y^{2} - 66 y + 400 = 0. \end{matrix}

Ekkor az egyenlet diszkriminánsa

66^{2} - 4 \cdot 9 \cdot 400 = 4356 - 14 400 < 0

, tehát valós gyök nincs.
Feladatunk egyetlen megoldása tehát

t = 24 {cm}^{2}

, s a meg nem adott két oldal

8

és

10

cm.

Megjegyzés: Észrevehető, hogy a háromszög három oldalára kapott értékek:

6

8

10

pythagorasi számhármast adnak, háromszögünk tehát Pythagoras tételének megfordítása alapján derékszögű.

Madarász Klára (Szeged, Tömörkény Ig. II. o. t.)

II. megoldás: A szóbanforgó háromszög derékszögű voltát fogjuk igazolni, s ebből számítjuk ki az oldalait és a területét.
Számítsuk ki az adott

5

cm sugarú körbe rajzolt

6

cm-es befogójú derékszögű háromszögbe írható körnek a sugarát (1. ábra).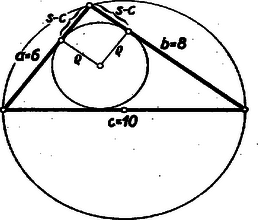

1. ábra

A háromszög átfogója

c = 2 r = 10 cm

, így Pythagoras-tétellel kiszámítva a másik befogó

8

cm. Derékszögű háromszögben a beírt kör sugara a derékszögű csúcstól a beírt kör érintési pontjáig terjedő szakasz hosszával egyezik, az érintőszakaszok hossza pedig (mint ismeretes) kifejezhető a félkerület s az oldalak különbségével. A jelen esetben a beírt kör sugara tehát

s - c = 12 - 10 = 2 cm

-rel egyenlő.
Igazolni fogjuk, hogy a körül írt kör

r

sugara, a beírt kör

ϱ

sugara és az

a

oldal egyértelműen meghatározzák a háromszöget. Az

a

oldal ugyanis a körülírt körben meghatározza már a háromszög szembenlevő

α

szögét (2. ábra).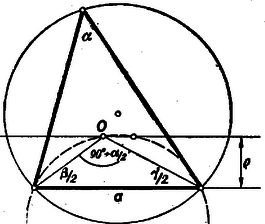

2. ábra

β

és

γ

szögek szögfelezőinek metszéspontjaként adódó, beírt kör

O

középpontjánál levő szög nagysága

180^{\circ} - \frac{β}{2} - \frac{γ}{2} = 180^{\circ} - \frac{β}{2} - \frac{γ}{2} - \frac{α}{2} + \frac{α}{2} = 180^{\circ} - 90^{\circ} + \frac{α}{2} = 90^{\circ} + \frac{α}{2}

, így

α

ismeretében megszerkeszthető az

a

oldal fölé az a

90^{\circ} \frac{α}{2}

látószögű kör, amelyen az

O

pont rajta van. Az

O

pont távolsága az oldaltól a megadott

ϱ

, így az

a

oldaltól

ϱ

távolságra haladó párhuzamos metszi ki

O

-t a megrajzolt látószögkörből. Az

O

pont ismeretében a szögfelezők megrajzolhatóak, s a szögek kétszeresével a háromszög-oldalak is.
Mivel a párhuzamos két pontban is metszheti a látószög-kört, ezért két háromszöget is kaphatunk. A kettő azonban az

a

oldal felezőmerőlegesére szimmetrikus, tehát egybevágó. Így valóban bizonyítottuk, hogy egy oldal, a beírt és körülírt kör sugara valóban egyetlen háromszöget határoznak meg.
Láttuk, hogy

r = 5 cm

esetén a

6

8

10

cm oldalú háromszögnél lesz a

ϱ

értéke

2

, ezzel tehát igazoltuk a szóbanforgó háromszög derékszögű voltát.
Az oldalakat már kiszámítottuk. A terület a befogók szorzatának fele:

24 cm^{2}

Börzsöny László (Bp. V., Eötvös g. I. o. t.)

Megjegyzések: 1. Látható, hogy az I. megoldásban követett gondolatmenettel a feladat akkor is megoldható, ha más számértékeket adunk meg. 2. A feladatunk egy szögfüggvényekkel (de szintén függvénytábla nélküli) történő megoldását (más számadatokkal ugyan) lásd a ,,Matematikai szakköri feladatgyűjtemény'' c. szakköri füzetben: 218. o. 587. feladat.