Kezdőlap


Feladat:	395. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Bender Cecilia , Kolonits Ferenc
Füzet:	1957/november, 112 - 113. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1957/január: 395. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A betűzést az 1. ábra mutatja.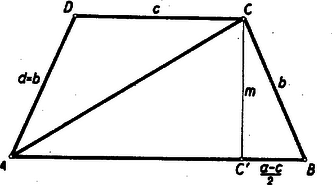

1. ábra

Állításunk igazolást nyert, ha megmutatjuk, hogy

\begin{matrix} e^{2} = b^{2} + {(\sqrt[]{a c})}^{2} = b^{2} + a c, \end{matrix}

mert ismeretes, hogy Pythagoras tétele megfordítható: minden háromszög derékszögű, amelynek oldalai kielégítik a pythagorasi egyenletet.

\begin{matrix} A C' = a - \frac{a - c}{2} = \frac{a + c}{2}, \end{matrix}

és így

\begin{matrix} e^{2} = {A C'}^{2} + m^{2} = {(\frac{a + c}{2})}^{2} + m^{2}, & (1) \\ b^{2} = {(\frac{a - c}{2})}^{2} + m^{2} . & (2) \end{matrix}

(1) és (2) különbsége

\begin{matrix} e^{2} - b^{2} = \frac{a^{2} + 2 a c + c^{2}}{4} - \frac{a^{2} - 2 a c + c^{2}}{4} = a c, \end{matrix}

ami bizonyítandó volt.

Bender Cecília (Bp. I., Szilágyi E. lg. II. o. t.)

II. megoldás: Rajzoljunk az egyik tompaszögű csúcs körül a szárral mint sugárral kört (a betűzést a 2. ábra mutatja).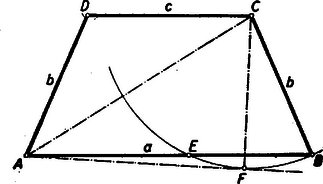

2. ábra

A hosszabb párhuzamos oldalon keletkező

E

metszéspontra

C E ∥ A D

, mert a

B E C

egyenlő szárú háromszögből és a trapéz egyenlő szárú voltából

\begin{matrix} C E B ∢ = C B E ∢ = D A C ∢ . \end{matrix}

Így

A E = D C = c

.
Ha a körhöz

A

-ból érintőt húzunk, akkor a keletkező

A C F

derékszögű háromszög két oldala az átlóval és a szárral egyenlő hosszúságú, az

A F

oldalra pedig az érintő mértani közép tulajdonsága szerint

\begin{matrix} A F = \sqrt[]{A B \cdot A E} = \sqrt[]{a c} . \end{matrix}

Ezzel igazoltuk az állítást, mivel három oldalból csak egyféle háromszög szerkeszthető.

Megjegyzés: A feladat állítása közvetlenül adódik Ptolemaios tételéből is. Mivel ugyanis minden egyenlő szárú trapéz húrnégyszög, a tétel szerint

\begin{matrix} e^{2} = b^{2} + a c, \end{matrix}

és ezt elegendő igazolni.

Kolonits Ferenc (Bp. VIII., Piarista g. II. o. t.)