| Feladat: | 393. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Bartha L. , Beke G. , Bender Cecilia , Bognár L. , Csanak Gy. , Czinege I. , Dániel G. , Elbert Á. , Endrődy T. , Fejes L. , Goldperger I. , Grallert F. , Gyene A. , Hadik Z. , Halász G. , Hornyánszky Tamás , Jalsovszky Gy. , Katona Gy. , Kesselyák M. , Kisvölcsey J. , Kolonits F. , Lassányi F. , Lefkovitsch S. , Losonczy L. , Magos A. , Márki Zay L. , Máthé Cs. , Mayer G. , Mihályffy L. , Mocskónyi M. , Molnár K. , Muszély Gy. , Náray Miklós (Bp.) , Náray Miklós (Győr) , Papp Éva , Perneczky G. , Raisz Klára , S. Nagy Erzsébet , Sima D. , Simonfai L. , Soós S. , Szász D. , Szatmári A. , Szatmári G. , Tamás Gyula (Bp.) , Tamás Gyula (Ózd) , Tatai Péter , Trón L. , Tusnády G. | ||
| Füzet: | 1957/október, 57 - 58. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Háromszögek nevezetes tételei, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1957/január: 393. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Jelöljük az középpontú beírt kör érintési pontját az átfogón -gyel, a oldalhoz írt középpontú, sugarú kör érintési pontját az befogón -vel (1. ábra). 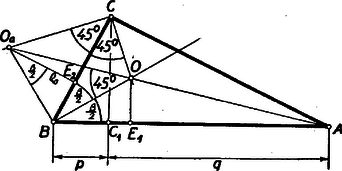 Be fogjuk bizonyítani, hogy . A belső és külső szögfelezők egymásra merőlegesek, azért a négyszög húrnégyszög, és így a kerületi szögek tétele szerint a . Tehát az derékszögű háromszög egyenlő szárú, vagyis . Mivel a mint merőleges szárú szög egyenlő -vel, azért a Hasonlóképpen
II. megoldás: A betűzést a 2. ábra mutatja. 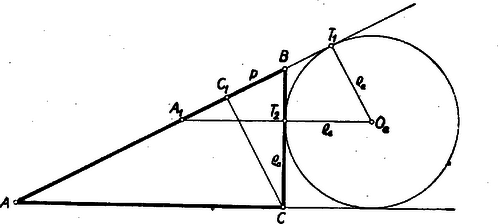
Továbbá Mivel a feltétel szerint , azért , tehát , és így (1) utolsó hasonlósága alapján Ugyanúgy miatt, -nek vetületére nézve
|