Kezdőlap


Feladat:	388. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Gavajda Pál , Tusnády Gábor
Füzet:	1957/május, 150 - 151. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Súlyvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/december: 388. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyenek a derékszögű háromszög oldalai $a < b < c$ , súlyvonalai $s_{a}$ , $s_{b}$ , $s_{c}$ .
Pythagoras tétele szerint

\begin{matrix} s_{a}^{2} = b^{2} + {(\frac{a}{2})}^{2}, s_{b}^{2} = a^{2} + {(\frac{b}{2})}^{2}, s_{c}^{2} = {(\frac{c}{2})}^{2} = \frac{a^{2} + b^{2}}{4} . \end{matrix}

Ebből kitűnik, hogy

a < b < c

esetén

s_{a} > s_{b} > s_{c}

.
Ha a súlyvonalakból szerkesztett háromszög derékszögű, akkor erre is érvényes Pythagoras tétele:

\begin{matrix} s_{a}^{2} = s_{b}^{2} + s_{c}^{2}, \end{matrix}

vagyis

\begin{matrix} b^{2} + \frac{a^{2}}{4} = a^{2} + \frac{b^{2}}{4} + \frac{a^{2} + b^{2}}{4}, \end{matrix}

ahonnan

\begin{matrix} b^{2} = 2 a^{2}, azaz b = a \sqrt[]{2} . \end{matrix}

Mivel okoskodásunk fordított sorrendben is elvégezhető, azért e szükséges feltétel elégséges is.
Tehát egy derékszögű háromszög súlyvonalaiból, mint oldalakból, szerkesztett háromszög, akkor és csak akkor derékszögű, ha az eredeti derékszögű háromszög befogóinak aránya:

1 : \sqrt[]{2}

Gavajda Pál (Bp. I. Petőfi g. I. o. t.)

II. megoldás: Egészítsük ki az

A C B

derékszögű háromszöget

A C B D

téglalappá, és jelöljük az

A C

C B

B D

és

B A

szakaszok felezőpontjait rendre

E

F

G

H

-val (lásd az ábrát).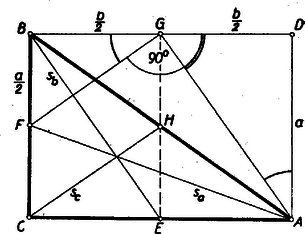

Mivel nyilvánvalóan

F G = C H = s_{c}

G A = B E = s_{b}

és

A F = s_{a}

, azért az

A F G_{▵}

oldalai az

A B C_{▵}

súlyvonalai.
E háromszögnek

s_{a}

-val szembenfekvő

G

csúcspontú szöge akkor és csak akkor derékszög, ha

\begin{matrix} B G F_{▵} \sim D A G_{▵}, \end{matrix}

ugyanis ekkor az egy ívvel jelölt szögek kiegészítik a két ívvel jelölt szöget derékszöggé.
Tehát ez esetben a befogók aránya

\begin{matrix} \frac{a}{2} : \frac{b}{2} = \frac{b}{2} : a, \end{matrix}

ahonnan

\begin{matrix} b = a \sqrt[]{2} . \end{matrix}

Tusnády Gábor (Sátoraljaújhely, Kossuth g. II. o. t.)