Kezdőlap


Feladat:	387. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: nehéz
Megoldó(k):	Bartha L. , Bayer Magda , Csanak G. , Dániel Gábor , Elbert Á. , Endrődy T. , Goldperger I. , Grallert F. , Gyene A. , Hornyánszky T. , Horváth F. , Kis Pap L. , Kisvölcsey J. , Kolonits F. , Kozmann Gy. , Krokovay Gizella , Magos A. , Mihályffy L. , Náray Miklós (Bp.) , Pátkai I. , Somkuti Piroska , Soós S. , Szabó Gy. , Szász D. , Szatmári G. , Tatai P. , Téry L. , Trón L. , Török S.
Füzet:	1957/május, 148 - 149. oldal		PDF \| MathML
Témakör(ök):	Négyzetek, Négyszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/december: 387. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Rajzoljuk meg az $A$ és $B$ pontok köré az $A B = 1$ sugarú $k_{1}$ és $k_{2}$ köröket. Mérjünk ezek kerületére $A$ , ill. $B$ -ből kiindulva háromszor az egységnyi húrt, nyerjük az $A'$ ( $A$ tükörképe $B$ -re nézve) és a $B'$ ( $B$ tükörképe $A$ -ra nézve) pontokat (1. ábra).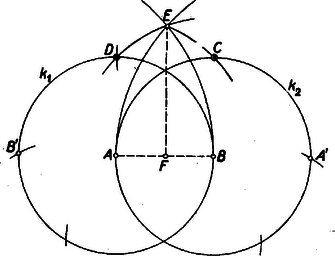

1. ábra

A'

és

B'

köré

A' A = B' B = 2

sugarú köröket rajzolva, ezek metszéspontja szolgáltatja az

E

pontot. Bebizonyítjuk, hogy

A E (= B E) = \sqrt[]{2}

, vagyis

A E

a keresett négyzet átlója.
Bizonyítás: Ha

A B

(ill.

A' B'

) felezőpontját

F

-fel jelöljük, akkor

E F ⊥ A' B'

. Pythagoras tétele alapján

E F^{2} = A' E^{2} - A' F^{2} = 2^{2} - {(\frac{3}{2})}^{2} = \frac{7}{4}

, s így

\begin{matrix} A E^{2} = E F^{2} + A F^{2} = \frac{7}{4} + \frac{1}{4} = 2. \end{matrix}

Tehát

A

körül

A E = \sqrt[]{2}

sugárral rajzolt kör metszi ki

k_{2}

-ből a négyzet

C

csúcsát. A

D

csúcs megszerkesztése most már kézenfekvő.
Természetesen ugyanígy szerkeszthető meg az

A B C D

négyzet

A B C' D'

tükörképe is.

Dániel Gábor (Bp. VIII., Piarista g. II. o. t.)

II. megoldás: Szerkesszük meg (mint az I. megoldásban) az

A

pontnak

B

-re vonatkozó

A'

tükörképét (2. ábra).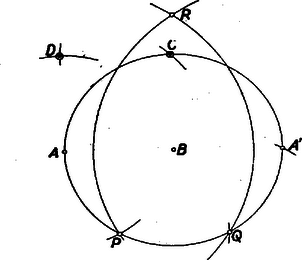

2. ábra

A A'

köríven legyenek a keletkező osztópontok

P

és

Q

(

A P = P Q = Q A' = A B = 1

A Q

(mint egy egységoldalú szabályos háromszög magasságának kétszerese, vagy mint az egységsugarú körbe írt szabályos háromszög oldala)

= \sqrt[]{3}

. Ha

A A'

, mint alap, fölé megszerkesztjük az

A A' R

egyenlő szárú háromszöget, ahol

A R = A' R = A Q = \sqrt[]{3}

, akkor a Pythagoras-tétel értelmében

\begin{matrix} B R = \sqrt[]{A R^{2} - A B^{2}} = \sqrt[]{3 - 1} = \sqrt[]{2} . \end{matrix}

A szerkesztés most már kézenfekvő (

A C = B R

Bayer Magda (Bp. XX., Bagi lg. II. o. t.)

Megjegyzés: Volt olyan megoldás, amely érintkező körök érintési pontját használta fel. Ez természetesen nem volt elfogadható, mert csak két kör különböző metszéspontjait tekintjük megszerkesztetteknek.