Feladat: 382. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Brodszky Ildikó ,  Papp Éva 
Füzet: 1957/április, 115 - 116. oldal  PDF  |  MathML 
Témakör(ök): Elsőfokú diofantikus egyenletek, Hossz, kerület, Terület, felszín, Téglalapok, Gyakorlat
Hivatkozás(ok):Feladatok: 1956/december: 382. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a téglalap két oldala x és y egész szám, ahol x≠y.
A feladat szerint

xy=2x+2y,
ahonnan
xy-2x-2y=0,xy-2x-2y+4=4,
vagyis
(x-2)(y-2)=4.

Tehát x-2 és y-2 két különböző osztója 4-nek. Pozitív egész x és y mellett a két tényező csak x=y=1 esetén negatív, ez esetben azonban a szorzat 1. Így csak 4 különböző, pozitív osztóit kell keresni. Ezek 1 és 4. Ha x-2=1 és y-2=4, akkor x=3, y=6. A két tényező felcserélésével x és y értéke felcserélődik.
 

Papp Éva (Bp. VIII., Ságvári lg. II. o. t.)

 

II. megoldás: Ha bármely téglalap belsejében az oldalakkal párhuzamos egyeneseket húzunk 1 cm távolságban, akkor az így nyert képkeret alakú idom (konkáv nyolcszög) területe 4 híján annyi cm2, ahány cm a téglalap kerülete, mert a téglalap kerületének minden cm-éhez tartozik a képkeret idom egy-egy 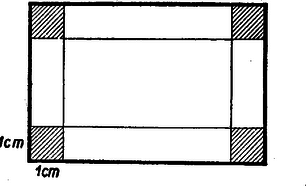cm2-re, de a 4 csúcsnál levő négyzetcentiméterek kétszer számítódnak (lásd az ábrát).
 

 

Feladatunknak tehát az a téglalap felel meg, amelyben a megmaradó belső, téglalap területe 4 cm2, és oldalai különböző egész számok. Ilyen csak az 1cm és 4cm oldalú téglalap, vagyis az eredeti téglalap oldalai 1+2=3cm, és 4+2=6cm.
 

Brodszky Ildikó (Bp. VIII., Ságvári lg. II. o. t.)