Kezdőlap


Feladat:	378. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bartha L. , Beke G. , Bender Cecilia , Bärnkopf R. , Elbert Á. , Endrődy T. , Ferenczy Kinga , Goldperger I. , Grallert F. , Gyene A. , Halász Gábor , Heinemann Irén , Jaross Anna , K. Nagy Ildikó , Kolonits F. , Losonczy L. , Madarász Klára , Magos A. , Máté Zs. , Mayer G. , Mihályffy L. , Papp Éva , Szabó Gy. , Szász D. , Szatmári A. , Tamás Gyula (Bp.) , Tamás Gyula (Ózd) , Téry L. , Trón L. , Tusnády G.
Füzet:	1957/április, 111 - 112. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Terület, felszín, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/november: 378. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Messe az $A$ csúcson át az $f_{c}$ -vel párhuzamosan húzott egyenes a $B C = a$ oldal meghosszabbítását egy $D$ pontban (lásd az ábrát).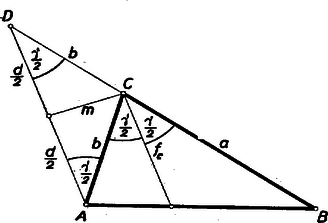

A szögekről leolvasható, hogy

C D = C A = b

. Az

A B C_{▵}

és

A C D_{▵}

területének aránya

a : b

, mert az

A

csúcsból kiinduló magasság e két háromszögben közös. Ha a területeket

t

, ill.

t_{1}

-gyel jelöljük, akkor tehát

t : t_{1} = a : b

, vagyis az

A B C_{▵}

keresett területe

\begin{matrix} t = \frac{a}{b} t_{1} . \end{matrix}

t_{1}

-et azonban könnyen ki tudjuk fejezni

f_{c}

-vel. Legyen az

A C D_{▵}

-ben az

A D

oldal

d

, az erre merőleges magasság

m

, akkor

\begin{matrix} d : f_{c} = (a + b) : a, vagyis d = \frac{(a + b) f_{c}}{a}, \end{matrix}

másrészt Pythagoras tétele alapján

\begin{matrix} m = \sqrt[]{b^{2} - {(\frac{d}{2})}^{2}} = \sqrt[]{b^{2} - \frac{{(a + b)}^{2} f_{c}^{2}}{4 a^{2}}} = \frac{1}{2 a} \sqrt[]{4 a^{2} b^{2} - {(a + b)}^{2} f_{c}^{2}} \end{matrix}

és így

\begin{matrix} t = \frac{a}{b} \cdot t_{1} = \frac{a}{b} \cdot \frac{d m}{2} = \frac{a}{b} \cdot \frac{(a + b) f_{c}}{4 a^{2}} \sqrt[]{4 a^{2} b^{2} - {(a + b)}^{2} f_{c}^{2}} = \\ = \frac{(a + b) f_{c}}{4 a b} \sqrt[]{4 a^{2} b^{2} - {(a + b)}^{2} f_{c}^{2}} . \end{matrix}

Halász Gábor (Bp. II., Rákóczi g. II. o. t.)

II. megoldás: Az

f_{c}

szögfelező két háromszögre bontja az

A B C_{▵}

-et, melynek

t

területe tehát egyenlő e két háromszög területének összegével, vagyis

\begin{matrix} 2 t = a b sin γ = a f_{c} sin \frac{γ}{2} + b f_{c} sin \frac{γ}{2} = (a + b) f_{c} sin \frac{γ}{2} . & (1) \\ sin γ helyében 2 sin \frac{γ}{2} cos \frac{γ}{2} -et írva, és sin \frac{γ}{2} -vel (sin \frac{γ}{2} \neq 0) \end{matrix}

osztva

\begin{matrix} 2 a b cos \frac{γ}{2} = (a + b) f_{c}, \end{matrix}

amiből

\begin{matrix} cos \frac{γ}{2} = \frac{(a + b) f_{c}}{2 a b} . \end{matrix}

(2)

Tehát (l)-ből a keresett

t

terület (2) figyelembevételével

\begin{matrix} t = \frac{(a + b) f_{c}}{2} \sqrt[]{1 - cos^{2} \frac{γ}{2}} = \frac{(a + b) f_{c}}{2} \sqrt[]{1 - \frac{{(a + b)}^{2} f_{c}^{2}}{4 a^{2} b^{2}}} = \\ = \frac{(a + b) f_{c}}{4 a b} \sqrt[]{4 a^{2} b^{2} - {(a + b)}^{2} f_{c}^{2}} . \end{matrix}

Heinemann Irén (Pécs, Leöwey K. lg. I. o. t.)