Kezdőlap


Feladat:	376. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Brodszky Ildikó , Kovács Margit
Füzet:	1957/április, 108 - 109. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Középpontos és egyéb hasonlósági transzformációk, Hossz, kerület, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/november: 376. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük az oldalakat $a$ , $b$ , $c$ , $d$ -vel, a kerületet $k$ -val, az átlókat $e$ , $f$ betűvel (1. ábra).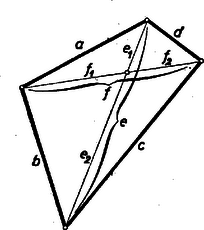

1. ábra

e

átló a négyszöget két háromszögre bontja. Mindegyikre felírjuk a háromszög oldalaira ismert egyenlőtlenséget:

\begin{matrix} e < a + b, e < c + d . \end{matrix}

Ezek összegezése adja

\begin{matrix} 2 e < a + b + c + d = k, vagyis e < \frac{k}{2} . \end{matrix}

(1)

Hasonló módon az

f

átló által létesített két háromszögből

\begin{matrix} f < \frac{k}{2} . \end{matrix}

(2)

(1) és (2) összege

\begin{matrix} e + f < k . \end{matrix}

(I)

Tekintsük most azt a négy háromszöget, amelyre a két átló a négyszöget bontja. Ennek a négy háromszögnek oldalai között szerepelnek az átlók részei:

e_{1}

és

e_{2}

, illetve

f_{1}

és

f_{2}

. Erre a négy háromszögre is írjuk fel a háromszög oldalaira vonatkozó egyenlőséget.

\begin{matrix} e_{1} + f_{1} & > a, \\ e_{2} + f_{1} & > b, \\ e_{2} + f_{2} & > c, \\ e_{1} + f_{2} & > d, \end{matrix}

amelyeknek összegezése adja

\begin{matrix} 2 (e_{1} + e_{2}) + 2 (f_{1} + f_{2}) = 2 (e + f) > a + b + c + d = k, \end{matrix}

vagyis

\begin{matrix} e + f > \frac{k}{2} . \end{matrix}

(II)

(I) és (II) így is írható

\begin{matrix} \frac{k}{2} < e + f < k, \end{matrix}

ami bizonyítandó, volt.

Kovács Margit (Szombathely, Savaria g. I. o. t.)

II. megoldás: A

k

kerületű

A B C D

négyszög oldalfelező pontjait rendre összekötve nyerjük az

A_{1} B_{1} C_{1} D_{1}

paralelogrammát (2. ábra), amelynek oldalai az

A C

, ill.

B D

átlók fele, tehát kerülete az átlók összege: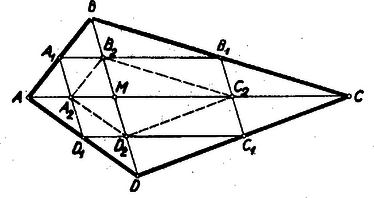

e + f

2. ábra

E paralelogramma oldalai metszik az

A B C D

négyszög átlóit az

A_{2}

B_{2}

C_{2}

D_{2}

pontokban. Az

A_{2} B_{2} C_{2} D_{2}

négyszög nem más, mint az

A B C D

négyszögnek, az átlók

M

metszéspontjára, mint hasonlósági centrumra vonatkozó

2 : 1

arányú kicsinyítése, és így kerülete

\frac{k}{2}

. Mivel konvex idomba írt konvex idom kerülete mindig kisebb az eredetinél, azért

\begin{matrix} \frac{k}{2} < e + f < k, \end{matrix}

amit bizonyítani kellett.

Brodszky Ildikó (Bp. VIII., Ságvári lg. II. o. t.)