Kezdőlap


Feladat:	354. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Sikabonyi György , Stark Gáspár
Füzet:	1957/január, 22 - 23. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Magasságvonal, Síkgeometriai számítások trigonometria nélkül háromszögekben, Koszinusztétel alkalmazása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/május: 354. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen az $A B C_{△}$ hegyesszögű (1. ábra).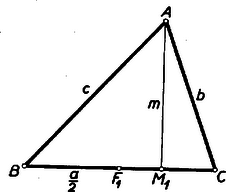

1. ábra

Írjuk fel a Pythagoras‐tételt az

A M_{1} B_{△}

, ill.

A M_{1} C_{△}

-ben:

\begin{matrix} c^{2} = {(\frac{a}{2} + M_{1} F_{1})}^{2} + m^{2}, \\ b^{2} = {(\frac{a}{2} - M_{1} F_{1})}^{2} + m^{2} . \end{matrix}

A második egyenletet kivonva az elsőből

\begin{matrix} c^{2} - b^{2} = 2 a \cdot M_{1} F_{1} . \end{matrix}

Ezzel állításunkat igazoltuk.
Teljesen hasonló a bizonyítás tompaszögű háromszögre is.
Megjegyzések: 1) Nyilvánvalóan igaz a tétel

b = c

esetben is, mert akkor

M_{1} = F_{1}

.
2)

γ = 90^{\circ}

esetén

M_{1} \equiv C

vagyis

M_{1} F_{1} = C F_{1} = \frac{a}{2}

és így

\begin{matrix} c^{2} - b^{2} = 2 a \cdot \frac{a}{2} = a^{2} . \end{matrix}

Bizonyított tételünk tehát a Pythagoras‐tétel egy általánosításának tekinthető általános háromszögre.

Sikabonyi György (Bp. VIII., Kandó híradásip. t. I. o. t.)

II. megoldás: Tekintsünk most tompaszögű háromszöget (2. ábra).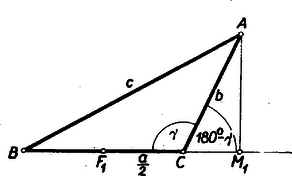

2. ábra

A cosinus‐tétel szerint

\begin{matrix} c^{2} - b^{2} = a^{2} - 2 a b cos γ, \\ F_{1} M_{1} = \frac{a}{2} + b cos (180^{\circ} - γ) = \frac{a}{2} - b cos γ . \end{matrix}

Ebből

\begin{matrix} 2 a \cdot F_{1} M_{1} = a^{2} - 2 a b cos γ, \end{matrix}

tehát

\begin{matrix} c^{2} - b^{2} = 2 a \cdot F_{1} M_{1} . \end{matrix}

A bizonyítás hegyesszögű háromszög esetén ugyanígy elvégezhető.

Stark Gáspár (Bp. VIII., Piarista g. II. o. t.)