Kezdőlap


Feladat:	339. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kolonits Ferenc , Vámos Péter
Füzet:	1956/november, 122 - 125. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Koszinusztétel alkalmazása, Gyakorlat
Hivatkozás(ok):	Feladatok: 1956/március: 339. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Berkes Jenő ,,A talpponti háromszögről'' c. cikkében (lásd az 1956. márciusi számban) kimutatja, hogy $m_{1} = 2 r cos α$ , ahol $r$ a háromszög köré írt kör sugara. Ha figyelembe vesszük, hogy

\begin{matrix} r = \frac{a b c}{4 t}, \end{matrix}

ahol

t

a háromszög területe, a cosinus-tétel szerint

\begin{matrix} cos α = \frac{b^{2} + c^{2} - a^{2}}{2 b c}, \end{matrix}

és

m = \frac{2 t}{a}

(ahol

a

m

-hez tartozó oldal), akkor

\begin{matrix} m m_{1} = \frac{2 t}{a} \cdot \frac{a b c}{2 t} \cdot \frac{b^{2} + c^{2} - a^{2}}{2 b c} = \frac{b^{2} + c^{2} - a^{2}}{2} . \end{matrix}

Megjegyzés: Ha

α

tompaszög, akkor vagy

m_{1}

-et negatívnak vesszük, vagy a jobboldal abszolút értékét tekintjük.

Kolonits Ferenc (Bp., VIII., Piarista g. I. o. t.)

II. megoldás: Az 1. ábra

A

-nál hegyesszögű háromszöget, a 2. ábra

A

-nál tompaszögű háromszöget tüntet fel, mindkettő egyben a betűzést is mutatja.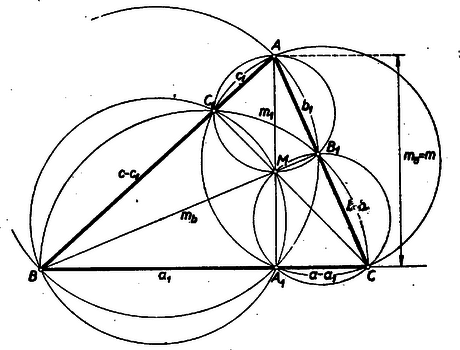

1. ábra

Mindkét ábrában

\begin{matrix} A B_{1} M ▵ \sim A A_{1} C ▵, \end{matrix}

mert derékszögű háromszögek, melyekben az

A

-nál fekvő hegyesszög közös, ill. csúcsszög.
Tehát

\begin{matrix} m_{1} : b_{1} = b : m, \end{matrix}

ahonnan

\begin{matrix} m m_{1} = b b_{1} . \end{matrix}

b_{1} = c cos α

, és így (

α

-t illetőleg a hegyesszög és tompaszög esetét összefoglalva)

\begin{matrix} m m_{1} = b c cos α = \frac{| b^{2} + c^{2} - a^{2} |}{2} . \end{matrix}

α

derékszög, akkor

M = A

, vagyis

m_{1} = 0

, és így

m m_{1} = 0

, amint azt a fenti képlet is mutatja

(b^{2} + c^{2} - a^{2} = 0)

Vámos Péter (Bp., II., Than Károly vegyip. t. II. o. t.)

III. megoldás: Tekintsük mindkét ábránkban az

M B_{1} C A_{1}

(a 2. ábrában

M B_{1} A_{1} C

), a

B C_{1} B_{1} C

(a 2. ábrában

B B_{1} C_{1} C

) stb. húrnégyszögek köré írt köröket.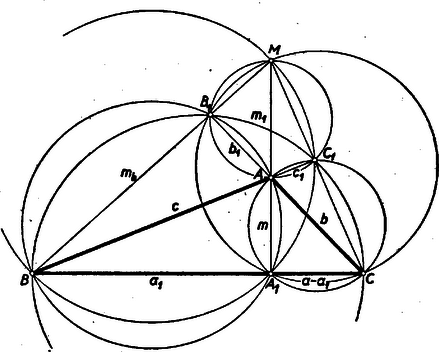

2. ábra

A

csúcspontból kiinduló szelőkre

\begin{matrix} m \cdot m_{1} = b \cdot b_{1} = c \cdot c_{1} . \end{matrix}

(1)

Hasonlóképpen az 1. ábrában a

C

-ből kiinduló szelőkre

\begin{matrix} b (b - b_{1}) = a (a - a_{1}), \end{matrix}

(2)

B

-ből kiinduló szelőkre

\begin{matrix} c (c - c_{1}) = a \cdot a_{1} . \end{matrix}

(3)

(2) és (3) összege

\begin{matrix} b^{2} + c^{2} - (b b_{1} + c c_{1}) = a^{2}, \end{matrix}

vagyis (1) figyelembevételével

\begin{matrix} b^{2} + c^{2} - 2 m \cdot m_{1} = a^{2}, \end{matrix}

ahonnan

\begin{matrix} m m_{1} = \frac{b^{2} + c^{2} - a^{2}}{2} . \end{matrix}

A 2. ábrában hasonlóképpen

\begin{matrix} b (b + b_{1}) = (a - a_{1}) a, \\ c (c + c_{1}) = a_{1} a, \end{matrix}

és így

\begin{matrix} b^{2} + c^{2} + (b b_{1} + c c_{1}) = a^{2}, \end{matrix}

ahonnan (1) figyelembevételével

\begin{matrix} m m_{1} = \frac{a^{2} - b^{2} - c^{2}}{2} . \end{matrix}