Feladat: 267. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bácsy Ernő ,  Csizmadia Lajos ,  Szabadits Ödön 
Füzet: 1955/december, 148 - 150. oldal  PDF  |  MathML 
Témakör(ök): Fizikai jellegű feladatok, Négyszögek geometriája, Síkgeometriai számítások trigonometria nélkül négyszögekben, Súlypont (tömegközéppont) meghatározása, Geometriai szerkesztések alkalmazása, Gyakorlat
Hivatkozás(ok):Feladatok: 1955/március: 267. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A súlypont és a súlyvonal fizikai értelmezéséből következnek alábbi tulajdonságaik.
1. Valamely idom súlypontján az idom mindegyik súlyvonala átmegy.
Fordítva: az idom súlypontja rajta van az idom mindegyik súlyvonalán.
2. Ha egy idomot két részre bontunk, s mindkettőnek megszerkesztjük a súlypontját, a két súlypont összekötő egyenes súlyvonala az eredeti idomnak. Ebből következik: ha egy idomból levágunk egy darabot, és megszerkesztjük az eredeti idom és a levágott idom súlypontját, ezek összekötő egyenese a csonkított idomnak is súlyvonala. Továbbá: ha egy idomhoz hozzáillesztünk egy másik idomot és megszerkesztjük a megnövelt idomnak és a hozzáillesztett idomnak a súlypontját, e két súlypont összekötő egyenese az eredeti idomnak is súlyvonala.
Ezek alapján a trapéznak tetszőleges számú súlyvonalát módunkban van megszerkeszteni és bármely két súlyvonal metszéspontja megadja a keresett súlypontot.
Néhány súlyvonal szerkesztését itt adjuk (1. ábra):

 
 
1. ábra
 

a) Hosszabbítsuk meg a trapéz szárait és egészítsük ki a trapézt háromszöggé. A kiegészítő háromszög és a megnövelt idom súlypontjának összekötő egyenese a trapéznak is súlyvonala; ez a két párhuzamos oldal felezőpontjának g összekötő egyenese.
b) Bontsuk a trapézt egyik átlójával két háromszögre, a két háromszög súlypontjának összekötő h egyenese szintén súlyvonala a trapéznak. (E súlyvonal párhuzamos a trapéz másik átlójával, ami abból következik, hogy a háromszög súlypontja a súlyvonalat 2:1 arányban osztja.)
c) Bontsuk szét a trapézt egy paralelogrammára és egy háromszögre, a paralelogramma középpontját kössük össze a háromszög súlypontjával. Ez az i egyenes is súlyvonala a trapéznak, stb.
 

Bácsy Ernő (Bp. VIII., Fazekas g. II. o. t.)
 

II. megoldás: Ha az S1 pontban m1 tömeget, az S2 pontban pedig m2 tömeget képzelünk egyesítve, akkor a két tömeg közös S súlypontja az S1S2 egyenesen van, a nagyobb tömeghez közelebb, és S az S1S2 szakaszt az m2 és m1 tömegek arányában osztja.
Bontsuk fel a trapézt egyik átlójával két háromszögre és szerkesszük meg ezek S1 és S2 súlypontját (2. ábra).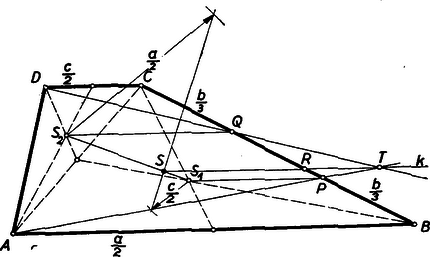
 
 
2. ábra
 

Homogén lemezek tömege, tehát e két háromszög tömege is, területükkel arányos. Miután azonban a két háromszög magassága egyenlő, az S1, és S2-be képzelendő tömegek a kérdéses háromszög alapjaival, tehát a párhuzamos oldalak hosszával arányosak. Eszerint az S súlypontot úgy is nyerhetjük, hogy az S1S2 szakaszt a párhuzamos oldalak c:a arányában osztjuk.
 

Csizmadia Lajos (Orosháza, Táncsics g. II. o. t.)
 

III. megoldás: A II. megoldás lehetővé teszi, hogy még két igen egyszerűen megszerkeszthető súlyvonalat találjunk. Az S1 és S2 és S pontoknak a párhuzamos oldalakkal párhuzamos vetületei a trapéz BC oldalán legyenek P, Q és R (2. ábra). A szerkesztés szerint P és Q három egyenlő részre osztja BC-t. Az R pont pedig ‐ mint láttuk ‐ a középső b3 hosszúságú PQ szakaszt c:a arányban osztja.
 

Osszuk megfordítva a BC oldalt a P és Q pontokkal 3 részre. Az AP és DQ egyenesek (2. ábra) messék egymást a T pontban. Azt állítjuk, hogy a T ponton át AB-vel párhuzamosan húzott k egyenes súlyvonal.
Az előbbiek alapján csak azt kell bebizonyítani, hogy a k egyenes a PQT▵ PQ oldalát olyan R pontban metszi, amelyre nézve
PRQR=ca.
De
ABP▵∼TRP▵,és ígyPR:PB=RT:AB,
vagyis
PR=PB⋅RTAB=b⋅RT3⋅a.
Hasonlóképpen nyerjük, hogy
QR=CQ⋅RTCD=b⋅RT3⋅c.
Tehát PRQR=ca, ami bizonyítandó volt.
 

IV. megoldás: A 2. ábráról könnyen leolvasható, hogy
BR=b3+ca+c⋅b3=b3(1+ca+c)=b3⋅a+2ca+c
és
CR=b3+aa+c⋅b3=b3(1+aa+c)=b3⋅2a+ca+c
tehát
BRCR=a+2c2a+c.

Ez a viszonyszám vezet a következő legegyszerűbb ‐ és ennélfogva a gyakorlatban leggyakrabban alkalmazott ‐ szerkesztéshez.
 
 
3. ábra
 

Hosszabbítsuk meg az AB oldalt az A-n túl, AU=c-vel, a CD oldalt ellenkező irányban CV=a-val (3. ábra), akkor UV újabb súlyvonal. Az
UF1S▵∼VF2S▵,
hasonlóságból ugyanis
F1SF2S=F1UF2V=a2+ca+c2=a+2c2a+c,
amiből az állítás következik.
 

Szabadits Ödön (Bp. XX., Kossuth g. I. o. t.)
 

Megjegyzés: A hiányos megoldásokban legtöbbnyire az indoklás hiányzott. Volt néhány helytelen megoldás is azzal az állítással, hogy a területfelező egyenes súlyvonal, holott ez csak akkor igaz, ha a félterületek súlypontjai a felező egyenestől egyenlő távolságra vannak. Helytelen megoldás az is, hogy a trapéz négy csúcspontjára ható párhuzamos irányú egyenlő erők támadópontját szerkesztjük. Ez a négy csúcspontból álló rendszer súlypontja, de nem a trapézé.