Kezdőlap


Feladat:	257. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Andrényi T. , B. Nagy O. , Bácsy E. , Bartók K. , Behringer T. , Csapody M. , Farkas L. , Farkas Marianna , Ferenczi Júlia , Fogarassy M. , Frivaldszky S. , Gelencsér L. , Grell M. , Hank Zs. , Jäger L. , Király Endre , Kismarty L. , Kluge Gy. , Konrády A. , Kovács L. , Kozma T. , Maczkó M. , Makkai M. , Paczolai Yvette , Pakucs J. , Parlagh Gy. , Rácz M. , Radács F. , Rockenbauer A. , Ruff I. , Ruppenthal P. , Soós T. , Stáhl J. , Strausz P. , Szebeni A. , Teőke Zsuzsa , Urbán J. , Vámos A. , Veér A. , Zaránd Pál , Zaránd Péter , Zichy A.
Füzet:	1955/november, 111 - 112. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1955/február: 257. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A keresett háromszög $c$ oldala az adott $M_{1}$ és $M_{2}$ pontokból derékszög alatt látszik, tehát $M_{1}$ és $M_{2}$ a $c$ oldal, mint átmérő fölé rajzolt Thales-körön van. E Thales-kör középpontja $M_{1}$ és $M_{2}$ -től egyenlő távolságra van, tehát az $M_{1} M_{2}$ szakaszt merőlegesen felező egyenes metszi ki a $c$ egyenesből a Thales-kör $F$ középpontját (1. ábra).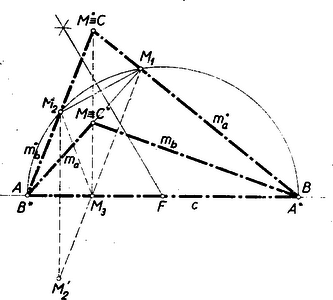

1. ábra

F M_{1} = F M_{2}

sugarú Thales-kör metszi a

c

egyenest az

A = B^{*}

és

B = A^{*}

pontokban. E jelölésnek megfelelően két megoldást nyerünk: az

A B C

és

A^{*} B^{*} C^{*}

háromszögeket.
Okoskodásunkban sehol sem használtuk fel azt a körülményt, hogy

M_{1}, M_{2}

c

egyenes ugyanazon vagy különböző oldalára esik, tehát szerkesztésünk mind a két esetben alkalmazható, és ‐ mint láttuk ‐ általában 2 megoldást ad.
Ha

M_{1}

és

M_{2}

c

oldal ugyanazon oldalára esik, akkor az egyik megoldás hegyesszögű a másik olyan tompaszögű háromszög, amelyben

c

a legnagyobb oldal. Ha

M_{1}

és

M_{2}

c

egyenes által el vannak választva, akkor mindkét megoldás tompaszögű és

c

egyikben sem a legnagyobb oldal. A feladatnak nincs megoldása, ha

M_{1} M_{2} ⊥ c

, mert ez esetben

M_{1} M_{2}

felező merőleges és

c

párhuzamosak. Nincs megoldás akkor sem, ha az

M_{1}

és

M_{2}

pontok a

c

egyenes két különböző oldalán, de

c

-től egyenlő távolságra vannak, mert ez esetben

A M_{1} ∥ B M_{2}

és

A^{*} M_{1} ∥ B^{*} M_{2}

. Ha az előbbi két eset egyszerre következik be, vagyis

M_{1}

és

M_{2}

c

-re, mint tengelyre, tükröshelyzetű, akkor az

F

pont a

c

bármelyik pontja lehet. Ez esetben tehát végtelen sok meóoldás van.

Király Endre (Nagykőrös, Arany János g. II. o. t.)

II. megoldás: Feladatunkat megoldottuk, ha megszerkesztettük

M_{1} M_{2} M_{3}

, talpponti háromszöget, vagyis a még hiányzó

M_{3}

pontot a

c

egyenesen. Ismeretes, hogy a magasságvonalak felezik a talpponti háromszög szögeit. Tehát, ha

M_{2}

-nek

c

-re vonatkozó

M_{2}

tükörképét összekötjük

M_{1}

-gyel, ez az összekötő egyenes metszi ki

c

-ből az

M_{3}

pontot (1. es 2. ábra).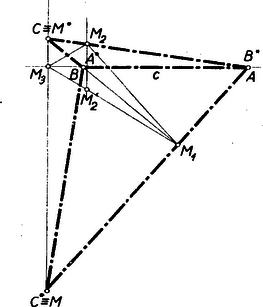

2. ábra

M_{1} M_{2} M_{3}

talpponti háromszögnek

M_{1}

- és

M_{2}

-ből kiinduló (belső és külső) szögfelezői metszik ki a

c

egyenesből az

A = B^{*}

és

B = A^{*}

pontokat, míg az egymással való metszéspontok szolgáltatják

C

, illetőleg

C^{*}

pontokat. Könnyű belátni, hogy

C

, ill.

C^{*}

A^{*} B^{*} C_{▵}^{*}

ill.

A B C_{▵}

magasságpontja, és mint ilyen szükségképpen rajta van az

M_{3}

-ban a

c

-re emelt merőlegesen.

Megjegyzés: Az

A (\equiv B^{*})

B (\equiv A^{*})

C (\equiv M^{*})

és

C^{*} (\equiv M)

pontok az

M_{1} M_{2} M_{3}

talpponti háromszögbe írt és hozzáírt köreinek középpontja.
Tanulságos a I. megoldásban végzett taglalást a II. megoldásban ‐ a talpponti háromszöggel kapcsolatban ‐ is elvégezni, de ezt már az olvasóra bízzuk.