Kezdőlap


Feladat:	250. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kozma Tibor
Füzet:	1955/október, 44 - 45. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Síkgeometriai számítások trigonometria nélkül háromszögekben, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1955/január: 250. matematika gyakorlat

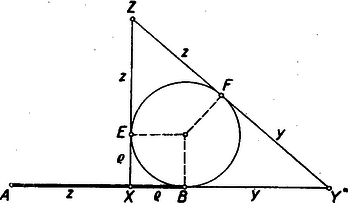
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Szerkesszünk az adott $A$ és $B$ pont közé a $λ = \frac{A X}{B X}$ arányhoz tartozó $X$ pontot, továbbá olyan $Z X Y^{*}$ derékszögű háromszöget, melynek egyik befogója $X Z = A B$ , beírt körének sugara $ϱ = X B$ . A háromszöget olyan helyzetben rajzoltuk (lásd ábrát), hogy $X Y^{*}$ befogója az adott egyenesre essék rá.

A beírt kör érintési pontjai

B

E

és

F

, amelyek az oldalakat

ϱ

y

és

z

hosszúságú szakaszokra bontják, úgyhogy

\begin{matrix} X B = X E = ϱ, Z E = Z F = z = A X, B Y^{*} = F Y^{*} = y . \end{matrix}

(1)

Alkalmazzuk a

Z X Y^{*}

háromszögre Pythagoras tételét

\begin{matrix} {(ϱ + y)}^{2} + {(ϱ + z)}^{2} = {(z + y)}^{2} \end{matrix}

(2)

Átalakítva és egyszerűsítve

\begin{matrix} ϱ (z + ϱ + y) = z y, \end{matrix}

(3)

amit (1) alapján így is írhatunk

\begin{matrix} X B \cdot A Y^{*} = A X \cdot B Y^{*}, \end{matrix}

(4)

ahonnan

\begin{matrix} \frac{A X}{X B} = \frac{A Y^{*}}{B Y^{*}} = λ . \end{matrix}

Eszerint az

Y^{*}

pont megegyezik az Appollonius kör másik metszéspontjával, a feladat szerint

Y

-nal jelölt ponttal.
Miután pedig

ϱ \neq X B

esetén az előbbitől különböző

Y^{*}

ponthoz jutunk,

ϱ \neq X B

esetén nem állhat fenn a (4) feltétel. Eszerint (4)-ből

ϱ = X B

következik.

Megjegyzés: Ahelyett, hogy a

Z X Y^{*}

háromszögre a Pythagoras-tételt alkalmaznánk, felhasználhatjuk az alábbi 251. gyakorlatban bizonyított állítást:

\begin{matrix} z y = \frac{(ϱ + y) (ϱ + z)}{2}, \end{matrix}

amelyből szintén az elözö megoldás (3) egyenletét nyerjük.

Kozma Tibor (Győr, Bencés g. II. o. t.)