Kezdőlap


Feladat:	243. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Gerőfy Klára , Grell Mihály , Kim Ju Szon , Kristóf László
Füzet:	1955/szeptember, 21 - 24. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/december: 243. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1. ábra mutatja.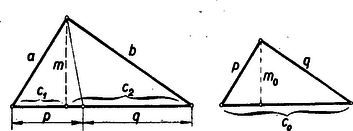

1. ábra

Ismeretes, hogy

\begin{matrix} m = \sqrt[]{c_{1} c_{2}} . \end{matrix}

(1)

c_{1}

és

c_{2}

-t kell az adott

p

és

q

-val kifejezni. Ez közvetlenül nem sikerül, de tudjuk

c_{1}

és

c_{2}

-t előbb a befogókkal kifejezni és aztán felhasználhatjuk a szögfelező tételét, mely szerint

\begin{matrix} \frac{p}{q} = \frac{a}{b} . \end{matrix}

(2)

Ismeretes továbbá, hogy

\begin{matrix} a^{2} = c_{1} c & (3) \\ b^{2} = c_{2} c . & (4) \end{matrix}

(3)-at elosztva (4)-gyel, (2) figyelembe vételével

\begin{matrix} \frac{c_{1}}{c_{2}} = \frac{a^{2}}{b^{2}} = \frac{p^{2}}{q^{2}}, \end{matrix}

(5)

másrészt

\begin{matrix} c_{1} + c_{2} = p + q . \end{matrix}

(6)

(5) és (6)-ból

c_{1}

és

c_{2}

, és így

c_{1} c_{2}

is meghatározható.

(5)-ből

\begin{matrix} c_{1} = \frac{c_{2} p^{2}}{q^{2}}, \end{matrix}

mely értéket (6)-ba helyettesítve

\begin{matrix} \frac{c_{2} p^{2}}{q^{2}} + c_{2} = p + q, \end{matrix}

amiből

\begin{matrix} c_{2} = \frac{(p + q) q^{2}}{p^{2} + q^{2}}, és így c_{1} = \frac{(p + q) p^{2}}{p^{2} + q^{2}} . \end{matrix}

Ezen értékeket (1)-be helyettesítve

\begin{matrix} m = \sqrt[]{\frac{{(p + q)}^{2} p^{2} q^{2}}{{(p^{2} + q^{2})}^{2}}} = \frac{(p + q) p q}{p^{2} + q^{2}} . \end{matrix}

Grell Mihály (Budapest, XVI., Corvin Mátyás g. II. o.)

II. megoldás: A szögfelező tétel alapján

\begin{matrix} \frac{p}{q} = \frac{a}{b}, vagyis a = λ p és b = λ q, \end{matrix}

(1)

ahol

λ

az arányossági tényező.
Írjuk fel a derékszögű háromszög kétszeres területét kétféleképpen:

\begin{matrix} 2 t = a b = c m . \end{matrix}

(1) felhasználásával és tekintetbe véve, hogy

c = p + q

\begin{matrix} λ^{2} p q = (p + q) m, \end{matrix}

amiből

\begin{matrix} m = λ^{2} \frac{p q}{p + q} . \end{matrix}

(2)

Már csak

λ^{2}

meghatározására van szükség. Ez Pythagoras tételének felhasználásával történhetik:

\begin{matrix} λ^{2} p^{2} + λ^{2} q^{2} = {(p + q)}^{2}, \end{matrix}

ahonnan

\begin{matrix} λ^{2} = \frac{{(p + q)}^{2}}{p^{2} - q^{2}} . \end{matrix}

λ^{2}

ezen értékét (2)-be helyettesítve

\begin{matrix} m = \frac{{(p + q)}^{2}}{p^{2} + q^{2}} \cdot \frac{p q}{p + q} = \frac{(p + q) p q}{p^{2} + q^{2}} . \end{matrix}

Kristóf László (Mosonmagyaróvár, Kossuth g. I. o. t.)

III. megoldás: A szögfelező tétel alapján a

p

és

q

befogókkal szerkesztett derékszögű háromszög hasonló az eredetihez (1. ábra).
A kis háromszög kétszeres területe

\begin{matrix} 2 t_{0} = p q = m_{0} c_{0} = m_{0} \sqrt[]{p^{2} + q^{2}}, \end{matrix}

amiből

\begin{matrix} m_{0} = \frac{p q}{\sqrt[]{p^{2} + q^{2}}} . \end{matrix}

A két háromszög hasonlósága miatt

\begin{matrix} m : m_{0} = c : c_{0}, \end{matrix}

vagyis

\begin{matrix} m = m_{0} \frac{c}{c_{0}} = \frac{p q}{\sqrt[]{p^{2} + q^{2}}} \cdot \frac{p + q}{\sqrt[]{p^{2} + q^{2}}} = \frac{(p + q) p q}{p^{2} + q^{2}} . \end{matrix}

Gerőfy Klára (Ózd, József Attila g. III o. t.)

IV. megoldás: Arra a kérdésre, hogy

≫

mekkora

≪

a magasság, szerkesztéssel is felelhetünk. Induljunk ki a

p + q = A B

átfogóból (2. ábra).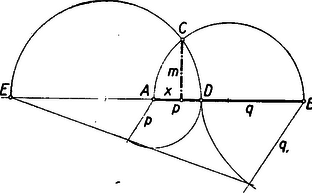

2. ábra

A derékszögű háromszög

C

csúcspontjának mértani helye, egyrészt az átfogó fölé rajzolt Thales-kör, másrészt az

A B

távolsághoz tartozó

\frac{p}{q}

aránynak megfelelő Apollonius-féle kör. E két kör metszéspontjának,

C

-nek távolsága az átfogótól a keresett

m

magasság.

Kim Ju Szon (Bp. I., Petőfi g. II. o. t.)

Megjegyzés: A szerkesztés alapján ki is számíthatjuk

m

-et a következő módon.
Az Apollonius‐körből adódik

\begin{matrix} \frac{E A}{E B} = \frac{D A}{D B} = \frac{p}{q}, azaz q \cdot E A = p (E A + p + q) . \end{matrix}

Innen

\begin{matrix} E A = \frac{p (p + q)}{q - p}, E B = \frac{q (p + q)}{q - p} . \end{matrix}

A húrok szeleteinek szorzatát a két kör közös húrjára alkalmazva

\begin{matrix} m^{2} & = x (p + q - x) = (p + q) x - x^{2}, \\ m^{2} & = (p - x) (E A + x) = \frac{p^{2} (p + q)}{q - p} - \frac{2 p^{2}}{q - p} x - x^{2} . \end{matrix}

A kettőt összehasonlítva nyerjük, hogy

\begin{matrix} \frac{q^{2} + p^{2}}{q - p} x = \frac{p^{2} (p + q)}{q - p}, x = \frac{p^{2} (p + q)}{p^{2} + q^{2}}, p + q - x = \frac{q^{2} (p + q)}{p^{2} + q^{2}}, \end{matrix}

és így

\begin{matrix} m^{2} = \frac{p^{2} (p + q)}{p^{2} + q^{2}} \cdot \frac{q^{2} (p + q)}{p^{2} + q^{2}}, m = \frac{p q (p + q)}{p^{2} + q^{2}} . \end{matrix}