Kezdőlap


Feladat:	232. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Dömötör Ákos , Pörczi József
Füzet:	1955/április, 109. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Súlyvonal, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/november: 232. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett egyenlőszárú háromszög alapja $A B$ . Adva van $γ$ és $s_{a} (= s_{b})$ . Mivel $A C = B C$ , azért $α = β = \frac{180^{\circ} - γ}{2}$ , továbbá ‐ $S$ -sel jelölve a súlypontot ‐ 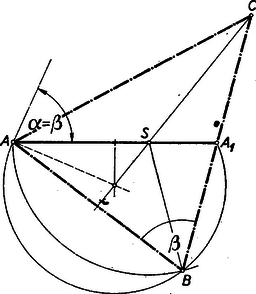$S A = S B = \frac{2}{3} s_{a}$ .
A szerkesztés menete tehát: Kiindulunk az $A A_{1} = s_{a}$ súlyvonalból, amelyen megszerkesztjük $S$ súlypontot (1. ábra).

1. ábra

B

pontból az

A A_{1}

súlyvonal

β

szög alatt látszik, továbbá

S B = S A

. Az

A A_{1}

szakaszhoz tartozó

β

látószög körívek és az

S

pont köré

S A

sugárral rajzolt kör közös pontjai szolgáltatják a

B

pontot. Mivel szükségképpen

β < 90^{\circ}

, azért a két mértani helynek mindig van, az

A

ponton kívül, még két közös pontja. Helyzetre nézve 2 megoldást kapunk, de ezek az

A A_{1}

súlyvonalra nézve tükrösök, tehát tulajdonképpen (alakra nézve) mindig egy és csakis egy megoldás van.

Dömötör Ákos (Bp. XI., József Attila g. II. o. t.)

II. megoldás. Az adott

γ

szög a keresett háromszög alakját meghatározza. Szerkesszünk tehát egy tetszőleges

A B' C'

egyenlőszárú háromszöget, melynek csúcspontja

C'

és csúcsszöge

γ

(2. ábr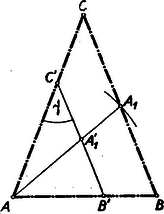a).

2. ábra

Legyen e háromszögnek az

A

pontból kiinduló súlyvonala

A A'_{1}

. E háromszöget az

A

centrumról az

A A_{1} : A A'_{1}

arányban megnagyobbítjuk (vagy kicsinyítjük), ahol

A A_{1} = s_{a}

az adott súlyvonal. Itt teljesen világosan látható, hogy mindig van egy és csakis egy megoldás.

Pörczi József (Pápa, Türr István g. II. o. t.)