Kezdőlap


Feladat:	227. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Árokszállási K. , Bartha Gyöngyi , Behringer T. , Csapody Miklós , Dobrovolszky A. , Egri Ibolya , Filinger L. , Fogarassy M. , Fuchs P. , Gáti Gy. , Gerőfy Klára , Hídvégi Z. , Kelemen J. , Klopfer S. , Kovács B. , Kovács K. , Kozma T. , Kristóf L. , Molnár I. , Pak To Ha , Pálinkás J. , Papp Z. , Rétey Piroska , Rockenbauer A. , Rudolf P. , Ruppenthal P. , Simók P. , Soós P. , Surányi Gy. , Szatmári Z. , Szilárd A. , Tóth L. , Ujhelly P. , zázrivecz L. , Zombori M.
Füzet:	1955/március, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Körérintési szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/október: 227. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mindenekelőtt észrevesszük, hogy a feladatnak 4-féle megoldása lehet. Ugyanis, ha azt a félsíkot, amely a szög szárának ugyanarra az oldalára esik, mint a másik szögszár, a szögszár belső oldalának a másik oldalát pedig külső oldalnak nevezzük, akkor a keresett körök $O_{1}$ és $O_{2}$ középpontjai a következőképpen helyezkedhetnek el: 1. $O_{1}$ és $O_{2}$ a belső oldalakon ‐ 2. $O_{1}$ a belső, $O_{2}$ a külső oldalon ‐ 3. $O_{2}$ a belső és $O_{1}$ a külső oldalon ‐ 4. $O_{1}$ és $O_{2}$ a külső oldalakon.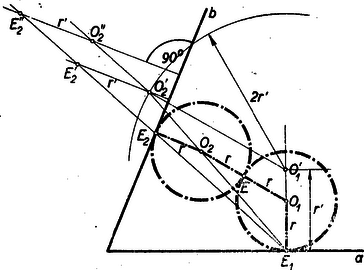
Tekintsük az 1. esetet megoldottnak. A betűzést az 1. ábra mutatja.

1. ábra

O_{1}

és

O_{2}

kör középpontok megszerkesztéséről van szó, ami egyértelmű azzal, hogy az

E_{1} O_{1} O_{2} E_{2}

tört vonalat, ill. négyszöget kell megszerkeszteni. Ezt közvetlenül megszerkeszteni nem tudjuk (egy kiegészített idom Apollonius‐féle kör felhasználásával meglehetősen komplikáltan szerkeszthető), de egyszerűen szerkeszthető egy hasonló (és egyben hasonló fekvésű) négyszög. Válasszuk hasonlósági centrumnak az

E_{1}

pontot. A feladat értelmében

E_{1} O_{1} : O_{1} O_{2} : O_{2} E_{2} = 1 : 2 : 1

, továbbá

E_{1} O_{1} ⊥ a

és

E_{2} O_{2} ⊥ b

A szerkesztés menete: az

E_{1}

-ben

a

-ra emelt merőlegesre mérjünk fel a belső oldalra egy tetszőleges

r' = E_{1} O'_{1}

távolságot. Ugyanezt a távolságot mérjük fel

E_{1} E_{2}

egyenesnek egy tetszőleges

E_{2}

pontjából, e pontból a

b

-re bocsátott merőlegesre

b

belső oldala által meghatározott irányban:

E'' O''_{2} = r'

. Ez utóbbi távolságot

E_{1} E_{2}

mentén önmagával párhuzamosan eltoljuk addig, amíg az

O''_{2}

rá nem esik az

O'_{1}

köré rajzolt

2 r'

sugarú körre. Jelöljük az

O''_{2}

-n át

E_{1} E_{2}

-vel húzott párhuzamos metszéspontját az említett körrel

O'_{2}

-vel, akkor

E_{1} O'_{1} O'_{2} E'_{2}

a hasonló és hasonló fekvésű négyszög.
Az

E_{1} O'_{2}

hasonlósági sugár metszi ki az

E_{2}

-ben

b

-re emelt merőlegesből az

O_{2}

pontot.

E_{2} O_{2} = r

.
Aszerint, amint az

r'

távolságot az

a

és

b

különböző oldalára mérjük, összesen 4 megoldást kapunk.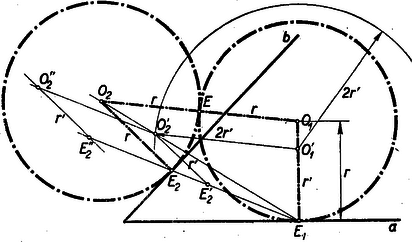

2. ábra

A 2. ábrán bemutatunk (kissé módosított felvételben) egy második megoldást (

O_{1}

belül,

O_{2}

kívül). Ugyanígy szerkeszthető a 3. és 4. megoldás is.

Csapody Miklós (Bp. VIII., Piarista g. II. o. t.)