| Feladat: | 224. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Ádám Antal , Bartha Gyöngyi , Behringer T. , Beregi P. , Csapody M. , Cserteg I. , Csillag A. , Frivaldszky S. , Fuchs P. , Gáti Gy. , Jókuti F. , Kozma Tibor , Makkai M. , Máté L. , Molnár J. , Nagy O. , Papp K. , Parlagh Gy. , Pogány Eörs , Rockenbauer A. , Ruppenthal P. , Soós T. , Stáhl J. , Szilárd A. , Újváry-Menyhárt Zoltán , Vámos A. , Wollner L. | ||
| Füzet: | 1955/március, 66 - 68. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Racionális számok és tulajdonságaik, Kör egyenlete, Pitagoraszi számhármasok, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1954/október: 224. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Mint ismeretes, az egyenlet az sugarú kör középponti egyenlete a derékszögű koordinátarendszerben. Legyen racionális szám. Ha sikerül bebizonyítani, hogy a kör a sík végtelen sok olyan pontján megy át, melynek koordinátái racionális számok, a feladatot megoldottuk. 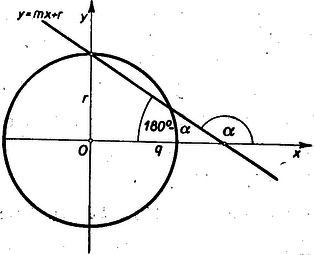 Rajzoljunk egy tetszőleges egyenest, mely az ordináta‐tengelyből szakaszt metsz ki (lásd ábrát). Ezen egyenes egyenlete Határozzuk meg a kör és ezen egyenes metszéspontjainak koordinátáit. E célból helyettesítsük be az értékét a kör egyenletébe: és akkor lesz racionális, ha az iránytangens racionális. . Tehát racionális, ha (az tengelyből levágott szakasz hossza) racionális. Mivel pedig az számegyenesen végtelen sok racionális abszcisszájú pont van, azért ilyen , ehhez tartozó egyenes és metszéspont is végtelen sok van, amivel a tételt bebizonyítottuk.
II. megoldás: Pythagorasi számhármasnak nevezzük azokat a pozitív egész számokból álló számhármasokat, melyekre a
Bizonyítható (lásd Számokról és alakzatokról című szakköri füzetet), hogy ha az és egészek, relatív prímek, és egyikük páros, másikuk páratlan, akkor az Legyen a felbontandó szám , ahol racionális szám. Szorozzuk meg (1)-et -tel Mivel racionális és , , egész, azért és is racionális. Ezzel -et felbontottuk végtelen sokféleképpen két racionális szám négyzetének összegére.
III. megoldás: Legyen a felbontandó racionális szám négyzete . Jelöljük az első racionális számot -szel, a másodikat -nal és írjuk az utóbbit alakban, ahol az és racionális paraméterek szabadon választhatók. Feladatunk értelmében Egy másodfokú egyenlet gyökei általában nem racionálisok, de ha az általános tag 0, akkor az egyik gyök 0, a másik pedig egy elsőfokú egyenlet gyöke, és mint ilyen, mindig racionális. Tehát ha -t úgy választjuk meg, hogy , akkor az
Megjegyzés: Igen sok megoldó jónak gondolta a következő rossz bizonyítást: Pythagoras tétele kimondja, hogy az átfogó négyzete egyenlő a befogók négyzetének összegével a derékszögű háromszögben. Thales tétele szerint viszont adott (jelen esetben racionális) átmérő fölé rajzolt félkör bármely pontját összekötve az átmérő két végpontjával derékszögű háromszöget kapunk, tehát végtelen sokszor bontható fel két racionális szám négyzetének összegére. Itt természetesen az a hiba, hogy semmi sem biztosít minket arról, hogy a kapott derékszögű háromszögek közül akár csak egyetlenegynek is két befogója racionális számmal mérhető. Ezt külön be kellene bizonyítani. Így ez a megoldás lényegében csak átfogalmazása a feladatnak. |