Feladat: 210. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Ádám A. ,  Bánhidy K. ,  Bartha Gyöngyi ,  Bayer J. ,  Benkő B. ,  Csák J. ,  Csapody M. ,  Csiszár I. ,  Deres J. ,  Deseő Katalin ,  Fekete J. ,  Frank Gy. ,  Frivaldszky S. ,  Gáti Gy. ,  Jakubovics Gy. ,  Kereszti I. ,  Makkai M. ,  Morelli Klára ,  Orlik P. ,  Parlagh Gy. ,  Perneczky L. ,  Rácz M. ,  Rázga T. ,  Ruppenthal P. ,  Siklósi K. ,  Soós T. ,  Stein J. ,  Surán G. ,  Szeidl B. ,  Szilárd A. ,  Udvari A. ,  Ulrich Z. ,  Ványai László ,  Vásárhelyi B. ,  Zsombok Z. 
Füzet: 1955/január, 13. oldal  PDF  |  MathML 
Témakör(ök): Körök, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1954/május: 210. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A betűzést az ábra mutatja.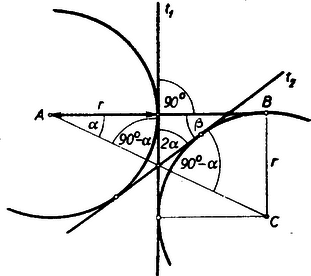

 
 

Mivel a két kör sugara egyenlő, azért a közös külső érintők az AB egyenessel ugyanazt az α szöget zárják be, mint az AC centrális, tgα=r2r=12 miatt α=26∘34'.
Az AB felezőpontjában AB-re emelt t1 merőleges a két körnek egyik közös belső érintője. Ez tehát AB-vel 90∘-os szöget zár be. A belső érintők az AC centrálissal tehát (90∘-α) szöget zárnak be, tehát egymással 180∘-2(90∘-α)=2α szöget, és így a t2-nek AB-vel bezárt szöge
β=90∘-2α=90∘-53∘08'=36∘52'.

Ványai László (Sátoraljaújhely, Kossuth g. II. o. t.)