Kezdőlap


Feladat:	186. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bánhidy K. , Bartha Gyöngyi , Behringer T. , Beke Gy. , Beliczky T. , Benkő B. , Csák J. , Csapody M. , Csiszár I. , Daróczy Z. , Deres G. , Deseő Katalin , Farkas L. , Fekete J. , Frank Gy. , Frivaldszky S. , Germadics V. , Győrősi P. , Harza Tibor , Heinemann Z. , Jakubovics J. , Katz T. , Leszler A. , Makkai M. , Mende I. , Mihalovits F. , Morelli Klára , Nagy Gy. , Orlik P. , Pak To Ha , Pauli A. , Pufa O. , Pölöskey I. , Rázga T. , Réti S. , Soós T. , Szabados J. , Szilárd A. , Ványai L. , Vásárhelyi L. , Zagg J. , Zsembery F. , Zsombok Z.
Füzet:	1954/november, 97 - 98. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/február: 186. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.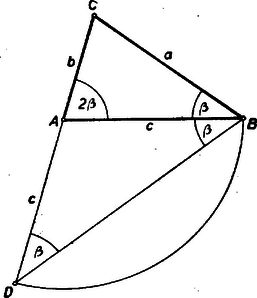

1. ábra

Ha az

A C = b

oldalt

A

-n túl

A D = A B = c

-vel meghosszabbítjuk, akkor a keletkezett

A B D

egyenlőszárú háromszög

A

csúcsánál fekvő külső szög

2 β

, és így a

B D

alapnál fekvő szögek mindegyike

β

. A

B C D ▵

-nek két szöge megegyezik az eredeti háromszög két szögével, és így

\begin{matrix} B C D ▵ \sim A C B ▵ . \end{matrix}

Tehát

\begin{matrix} a : (b + c) = b : a, \end{matrix}

vagyis

\begin{matrix} a^{2} = b (b + c) . \end{matrix}

(1)

b

oldal szerkesztését a 2. ábra mutatja.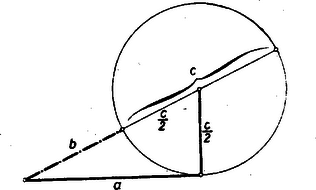

2. ábra

Itt hivatkozhatunk arra az ismeretes tételre, hogy az érintő szakasz mértani középarányos az érintő végpontjából húzott szelőn keletkezett két szelet között, de Pythagoras tételének ismerete is elegendő. Ugyanis (1) mindkét oldalához

{(\frac{c}{2})}^{2}

-t hozzáadva

\begin{matrix} a^{2} + {(\frac{c}{2})}^{2} = b^{2} + b c + {(\frac{c}{2})}^{2} = {(b + \frac{c}{2})}^{2}, \end{matrix}

tehát

\begin{matrix} b = \sqrt[]{a^{2} + {(\frac{c}{2})}^{2}} - \frac{c}{2} . \end{matrix}

A megoldhatóság szükséges és elégséges feltétele, hogy

a + b > c

, vagyis

b > c - a

.
Írjuk az (1) jobboldalán

b

helyébe a nálánál kisebb

(c - a)

-t:

\begin{matrix} a^{2} > (c - a) (2 c - a) = 2 c^{2} - 3 a c + a^{2}, \end{matrix}

vagyis

\begin{matrix} 3 a c > 2 c^{2}, \end{matrix}

ahonnan (tekintve, hogy

a > 0

c > 0

)

\begin{matrix} a > \frac{2}{3} c . \end{matrix}

Harza Tibor (Székesfehérvár, József A. g. II. o. t.)