Kezdőlap


Feladat:	183. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Behringer T. , Beke Gy. , Benkő B. , Csapody M. , Csiszár I. , Györösi Péter , Harza T. , Kozma Tibor , Makkai M. , Parlagh Gy. , Rázga T. , Szabados G. , Szeidl B. , Vásárhelyi B. , Zsombok Z.
Füzet:	1954/október, 44 - 46. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1954/február: 183. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a két egyenes $e_{1}$ és $e_{2}$ . Miközben a $P$ pont egy, a két egyenes $A$ metszéspontján átmenő, $k$ kört írt le, tükörképei $P_{1}$ , ill. $P_{2}$ ezen $k$ körnek tükörképeit: a $k_{1}$ és $k_{2}$ kört írják 1e (1. ábra).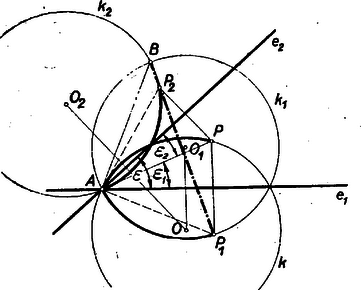

1. ábra

k_{1}

és

k_{2}

körök

A

-n kívül még egy

B

pontban metszik egymást, mely

B

pont a

k

k_{1}

k_{2}

körökkel és az

A

ponttal együtt rögzített állandó.
Ha kimutatjuk, hogy a

B

P_{1}

és

P_{2}

pontok egy egyenesen vannak, akkor tételünket bebizonyítottuk.
Két esetet kell megkülönböztetni:
1.

P_{1}

és

P_{2}

A B

egyenesnek ugyanazon az oldalán vannak (1. ábra), vagy
2. az

A B

egyenes a

P_{1}

és

P_{2}

, pontokat szétválasztja (2. ábra).
Mivel a tükrözés folytán

\begin{matrix} \hat{A P} = {\hat{A P}}_{1} = {\hat{A P}}_{2} \end{matrix}

(1)

(1. ábrán vastagítva), azért az
1. esetben (1. ábra) a kerületi szögek tétele alapján

A B P_{1} ∢ = A B P_{2} ∢

. E két egyenlő szögnek azonban az

A B

szára közös, tehát közös a másik szára is, vagyis

B P_{1}

és

B P_{2}

azonos egyenesek.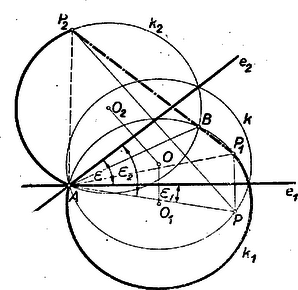

2. ábra

A 2. esetben

A B P_{1} ∢

és

A B P_{2} ∢

olyan köríveken nyugvó kerületi szögek (a 2. ábrán vastagítva), amelyeknek összege (1) alapján egy teljes kör és így ismét a kerületi szögek tétele alapján

\begin{matrix} A B P_{1} ∢ + A B P_{2} ∢ = 180^{\circ}, \end{matrix}

ami ismét azt jelenti, hogy a

B

P_{1}

és

P_{2}

pontok egy egyenesen feküsznek. Ezzel bebizonyítottuk, hogy a

P_{1} P_{2}

egyenes a

B

pont körül forog.

Györösi Péter (Bp., IV., Könyves Kálmán g. II. o. t.)

II. megoldás: Jelöljük az

e_{1}

és

e_{2}

egyenesek szögét

ε

-nal. A tükrözés folytán

A P = A P_{1} = A P_{2}

, vagyis a

P_{1} A P_{2} ▵

egyenlő szárú és a

P_{1} ∢ = P_{2} ∢

. Az

A

csúcsnál fekvő szögéről meg fogjuk mutatni, hogy (a

P

helyzetétől független) állandó. Ugyanis, ha az

A P

egyenesnek az

e_{1}

illetőleg

e_{2}

vel bezárt hegyes szögeit

ε_{1}

és

ε_{2}

-vel jelöljük, akkor a tükrözés miatt

P A P_{1} ∢ = 2 ε_{1}

és a

P A P_{2} ∢ = 2 ε_{2}

, vagyis az I. esetben, amikor a

P

a hegyesszög szárai között van (1. ábra)

\begin{matrix} P_{1} A P_{2} ∢ = 2 ε_{1} + 2 ε_{2} = 2 (ε_{1} + ε_{2}) = 2 ε, \end{matrix}

míg a II. esetben, mikor a

P

a tompaszög szárai között van (2. ábra)

\begin{matrix} P_{1} A P_{2} ∢ = 2 ε_{2} - 2 ε_{1} = 2 (ε_{2} - ε_{1}) = 2 ε . \end{matrix}

P_{1} A P_{2} ▵

A ∢

-e tehát mindenkor

2 ε

állandó nagyságú, következésképpen a

P_{1} ∢ = P_{2} ∢

is állandó nagyságú, vagyis

P_{1} A P_{2}

egyenlőszárú háromszögek egymásközt mind hasonlók. (A

P

pont mozgásával a

P_{1} A P_{2} ▵

nagyságra változik, de alakra változatlan marad.)

A P_{1} P_{2} ∢ = A P_{2} P_{1} ∢

állandó nagyságú szögek

P_{1} A

, ill.

P_{2} A

szárának a

k_{1}

és

k_{2}

körökkel való metszéspontja az

A

pont rögzített, tehát a másik száruknak (

P_{1} P_{2}

, illetőleg

P_{2} P_{1}

) metszéspontja a

k_{1}

és

k_{2}

körökkel egy-egy szilárd pont az illető körön. A változó

P_{1} P_{2}

egyenes csak úgy mehet át állandóan

2

szilárd ponton, ha a 2 szilárd pont egybeesik a

k_{1}

és

k_{2}

közös

B

pontjában.

Kozma Tibor (Győr, Czuczor Gergely g. I. o. t.)