Kezdőlap


Feladat:	168. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bánhidy Kálmán , Makkai Mihály
Füzet:	1954/május, 139 - 141. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/december: 168. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Ismeretes tétel, hogy egy háromszögben nagyobb egyenlő, ill. kisebb oldallal szemben nagyobb, egyenlő ill. kisebb szög fekszik.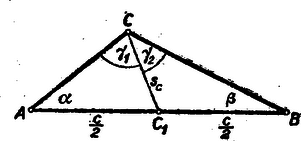

1. ábra

Ennek alapján ha

s_{c}

γ

szöget

γ_{1}

és

γ_{2}

szögekre osztja (1. ábra), akkor az

A C_{1} C_{▵}

-ből

\begin{matrix} \frac{c}{2} ⋛ s_{c}, aszerint, amint γ_{1} ⋛ α, \end{matrix}

(1)

ugyanígy a

B C_{1} C_{▵}

-ből

\begin{matrix} \frac{c}{2} ⋛ s_{c}, aszerint, amint γ_{2} ⋛ β \end{matrix}

(2)

(1) és (2) összeadásából

\begin{matrix} c ⋛ 2 s_{c}, aszerint, amint γ_{1} + γ_{2} ⋛ α + β \end{matrix}

(3)

γ_{1} + γ_{2} = γ

és

α + β + γ = 180^{\circ}

, azért a (3) egyenértékű azzal, hogy

\begin{matrix} γ ⋛ 90^{\circ} . \end{matrix}

Tehát tényleg

\begin{matrix} s_{c} ⋛ \frac{c}{2}, aszerint, amint γ ⋚ 90^{\circ} . \end{matrix}

Makkai Mihály (Bp., V., Eötvös g. I. o. t.)

II. megoldás: Egy

A B C

derékszögű háromszögben rajzoljuk meg az

s_{c}

súlyvonalat és a háromszög köré írt kört, amely nem más, mint az átfogó fölé rajzolt Thales-kör, amelynek középpontja az

s_{c}

súlyvonal végpontja

C_{1}

, és sugara

s_{c} = \fra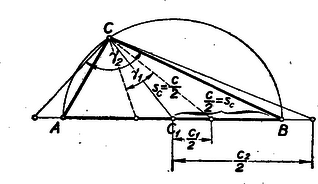c{c}{2}

. (2. ábra.)

2. ábra

Rögzítsük a

c

oldal hordozóját és azon a

C_{1}

pontot a köréje rajzolt

s_{c}

sugarú körrel. A

C

pont e körnek bármely pontja lehet.
Nyilvánvaló, hogy amíg

\begin{matrix} \frac{c}{2} = s_{c}, γ = 90^{\circ}, \end{matrix}

de ugyancsak evidens az ábrából, hogy ha

\begin{matrix} \frac{c_{1}}{2} < s_{c}, ill. \frac{c_{2}}{2} > s_{c}, \end{matrix}

akkor

\begin{matrix} γ_{1} < 90^{\circ}, ill. γ_{2} > 90^{\circ} . \end{matrix}

Bánhidy Kálmán (Debrecen, Ref. gimn. II. o. t.)