Feladat: 161. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bánhidy K. ,  Bayer J. ,  Beke Gy. ,  Benkő B. ,  Berár I. ,  Boga B. ,  Csapó Zs. ,  Csapody M. ,  Csete Gy. ,  Csiszár I. ,  Daróczy Z. ,  Deseő Katalin ,  Döbrösy A. ,  Fodor M. ,  Forgó G. ,  Frivaldszky S. ,  Germadics Ilona ,  Geszti T. ,  Gulácsy Sára ,  Gulyás Gyöngyi ,  Györösi P. ,  Harza T. ,  Imre T. ,  Jakubovics J. ,  Jordán Gy. ,  Kaiser Emilia ,  Kálmán László (Eszt.ergom) ,  Kalmár Gy. ,  Kardos Erzsébet ,  Katz T. ,  Kereszti I. ,  Kiss S. ,  Koltai H. ,  Kozma T. ,  Lukács P. ,  Makkai M. ,  Mészáros I. ,  Mihalovits F. ,  Nagy J. ,  Németh Zsuzsanna ,  No Mjang Gi ,  Orlik P. ,  Perneczky L. ,  Poór I. ,  Rázga T. ,  Rudolf P. ,  Szabados J. ,  Szabó A. ,  Szabó G. ,  Szathmáry Z. ,  Szeidl B. ,  Takács B. ,  Tihanyi I. ,  Tisza Magdolna ,  Tódor T. ,  Varga Margit ,  Vásárhelyi B. ,  Veres S. ,  Zsemberi F. ,  Zsombok Z. 
Füzet: 1954/április, 112 - 113. oldal  PDF  |  MathML 
Témakör(ök): Terület, felszín, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):Feladatok: 1953/november: 161. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Tekintsük a feladatot megoldottnak olyan esetben, amikor a Q pont az A csúccsal szemközt fekvő a oldalon van (1. ábra). A háromszög területét jelöljük t-vel és az oldalfelező pontok legyenek rendre 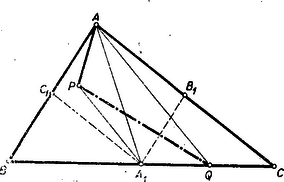A1, B1, C1,.

 
 
1. ábra
 

Az APQC négyszög területe, tehát a feltétel szerint t2, az AA1C▵ területe pedig szükségképpen t2. E két idomnak egy közös része az ACQ▵, tehát területileg AQP▵=AQA1▵, amiből következik, hogy PA1∥AQ. Nyilvánvaló, hogy a P pont ebben az esetben csak az AB1A1C1 paralelogrammán belül lehet.
De megfordítva is, ha a P pont az AB1A1C1 paralelogrammán belül van, akkor megszerkesztve az A ponton át PA1-gyel húzott párhuzamost ez a szemközti a oldalból nyilván a feltételeknek megfelelő Q pontot metszi ki. Ez az 1. típusú megoldás: a háromszög egy konvex és egy konkáv négyszögre bomlik.
b) Tekintsük most azt az esetet, amikor P pl. az A1BC1▵-ben van. Ekkor Q mint láttuk, nem lehet a-n, de nyilván c-n sem, tehát Q a b-n van (2. ábra). Jelöljük az AP egyenes metszéspontját az A1C1 szakasszal 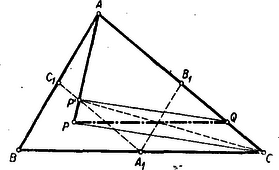P'-vel.
 
 
2. ábra
 

Az APQ▵ területe a feltétel szerint, az AP'C▵ területe pedig szükségképpen t2. A két egyenlő területű háromszögnek egy közös része az AP'Q▵, és így területileg P'QP▵=P'QC▵, vagyis PC∥P'Q.
Tehát a szerkesztés menete, ha a P pont nincs a fenti paralelogramma belsejében: Meghatározzuk az AP metszéspontját P'-t a jelzett paralelogrammával P'-n át PC illetőleg PB-vel (aszerint, amint P az A1C1 ill. A1B1 oldalon van) húzott párhuzamos metszi ki a b ill. c oldalon a keresett Q pontot. Ez a 2. típusú megoldás: a háromszög egy háromszögre és egy konkáv ötszögre bomlik.
A háromszög egy csúcspontját kiragadva, tehát mindig van 1 és csakis 1 megoldás. Ha mindhárom csúcspontot tekintjük, akkor minden P ponthoz mindig találunk 3 és csakis 3 megoldást. Ha a P pont az A1B1C1 háromszög belsejében van, akkor mind a három megoldás 1. típusú. Különben csak egy megoldás 1. típusú (a P-hez legközelebbi csúcspontra vonatkozó), a másik kettő 2. típusú. Ha a P pont rajta van az A1B1C1 kerületén, akkor két megoldás egybeesik úgy, hogy Q az adott háromszög egy-egy csúcspontjába kerül (a háromszög felbomlik egy háromszögre, és egy konkáv négyszögre), a harmadik megoldás 1. típusú. Ha P rajta van valamely súlyvonalon, akkor az egyik Q pont a súlyvonal talppontja (az eredeti háromszög két háromszögre bomlik), végül ha P azonos a súlyponttal akkor a három Q pont azonos az A1, B1, C1 pontokkal.