Kezdőlap


Feladat:	155. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke Gy. , Csiszár I. , Deseő Katalin , Germadics V. , Györösi P. , Jakubovits J. , Kalmár Gy. , Rázga T. , Takács B. , Závody A. , Zsombok Z.
Füzet:	1954/április, 108. oldal		PDF \| MathML
Témakör(ök):	Kör (és részhalmaza), mint mértani hely, Négyszögek szerkesztése, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/október: 155. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Képzeljük a feladatot megoldottnak. A betűzést az ábra mutatja, melyben tekintsük az $A_{1} B_{1} C_{1} D_{1}$ megoldást.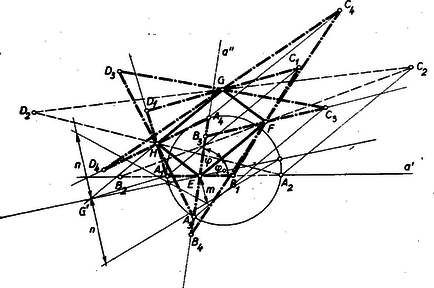

Az adott

E

F

G

oldalfelező pontok egyértelműen meghatározzák a negyedik oldalfelező pontot, a

H

-t is, mert ismeretes, hogy

E F G H

paralelogramma. E paralelogramma oldalai párhuzamosak az átlókkal. Tehát

E F ∥ A C

, és így az

E

csúcsponton átmenő és

E F

-fel adott

φ

szöget bezáró

a'

egyenes az

A B

négyszögoldal hordozója.
Tükrözzük a

D_{1} G

szakaszt a

H

ponton át. Akkor az így nyert

A_{1} G'

szakaszról tudjuk, hogy

A_{1} G' ♯ D_{1} G

. A keletkezett

G' E A_{1} ▵

-ben

A_{1} E : A_{1} G' = A_{1} E : D_{1} G = A_{1} B_{1} : C_{1} D_{1} = q

.
Ha a

q

viszonyszámot két adott szakasz:

m

és

n

arányával

(q = \frac{m}{n})

képzeljük megadva, akkor az

A_{1}

pont rajta van a

G' E

szakaszhoz tartozó azon Apollonius-körön, melynek

A

pontjaira nézve

A E : A G' = m : n

.
A szerkesztés menete tehát: kiindulunk a megadott

E F G H

paralelogrammából. Megszerkesztjük az

E

ponton át az

A B

oldal hordozóját, amely az

E F

egyenessel az adott

φ

szöget zárja be. Ha

φ \neq 90^{\circ}

, akkor két ilyen egyenes van:

a'

és

a''

. A

G

pontnak a

H

-ra vonatkozó

G'

tükörképét összekötjük az

E

ponttal. A

G' E

egyenesen megszerkesztjük az adott

m

és

n

szakaszok felhasználásával a fent említett Apollonius-kör átmérőjét és középpontját. (Az ábrában betűzetlen nullkörök.) Az így megszerkesztett Apollonius-kör metszi ki az

a'

és

a''

egyenesekből a keresett

A_{1} A_{2}

ill.

A_{3} A_{4}

csúcspontokat, amelyeknek birtokában a másik

3

csúcspont megszerkesztése esetről-esetre tükrözéssel már triviális.
A megoldások száma

(ha φ \neq 90^{\circ})

tehát

4

3

2

1

vagy

0

aszerint, amint az Apollonius-kör az

a'

és

a''

egyeneseket

2

‐

2

különböző,

2

különböző és

2

egybeeső,

2

‐

2

egybeeső pontban metszi, vagy pedig az egyik egyenest nem metszi és ugyanakkor a másik egyenest

2

különböző,

2

egybeeső pontban, vagy nem metszi. Ha

φ = 90^{\circ}

, akkor

a' = a''

és a megoldások száma:

2

1

, vagy

0

.
A megoldások között lehetnek konvex négyszögek

(A_{1} B_{1} C_{1} D_{1})

, konkáv négyszögek (

A_{3} B_{3} C_{3} D_{3}

és

A_{4} B_{4} C_{4} D_{4}

) és hurkolt négyszögek is

(A_{2} B_{2} C_{2} D_{2})

Megjegyzés: Az Apollonius-kör felhasználása helyett az

A E G'

háromszögek hasonlósági transzformáció segítségével is szerkeszthetők.