Kezdőlap


Feladat:	153. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Csiszár I. , Farkas L. , Fekete J. , Imre T. , Jordán Gy. , Morelli Klára , Rázga T. , Szeidl B.
Füzet:	1954/április, 106 - 107. oldal		PDF \| MathML
Témakör(ök):	Alakzatok hasonlósága, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/október: 153. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.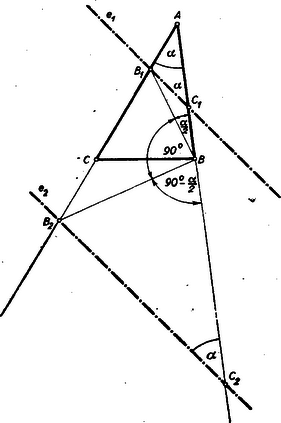

1. ábra

Mivel a feladat értelmében

A B_{1} = B_{1} C_{1}

, azért az

A C_{1} B_{1} ∢

is egyenlő

α

-val. Ez utóbbi szög azonban külső szöge a

B_{1} C_{1} B

egyenlőszárú háromszögnek, tehát a

C_{1} B B_{1} ∢ = \frac{α}{2}

. A

B_{2} C_{2}

második megoldásra nézve

A B_{2} = B_{2} C_{2}

miatt a

C_{2}

-nél levő szög is

α

, vagyis a

B C_{2} B_{2}

egyenlőszárú háromszögben a

C_{2} B B_{2} ∢ = 90^{\circ} - \frac{α}{2}

és így a

B_{1} B B_{2} ∢ = 90^{\circ}

.
A megoldás menete tehát: Megszerkesztjük a

B

pontból kiinduló azokat az egymásra merőleges félegyeneseket, amelyek közül az egyik a

B A

szakasszal

\frac{α}{2}

szöget zár be és amelyek a szemközt fekvő

b

oldalt metszik. E metszéspontok lesznek a keresett

B_{1}

ill.

B_{2}

pontok. A

C_{1}

ill.

C_{2}

pontokat egyszerűen

B_{1} C_{1} = B_{1} A

ill.

B_{2} C_{2} = B_{2} A

alapján nyerjük. Tehát általában két egymással párhuzamos

e_{1}

és

e_{2}

megoldást kapunk.
Ha

α = 60^{\circ}

, vagyis

\frac{α}{2} = 30^{\circ}

, akkor

B B_{1} ⊥ b

és így

B B_{2} ∥ b

, tehát a

B_{2}

pont a végtelenbe kerül. Ez esetben tulajdonképpen csak egy megoldásról beszélhetünk. Ugyanígy

B B_{1} ∥ b

, ha

α = 120^{\circ}

, mely esetben szintén csak egy megoldás van. Ha

α = 90^{\circ}

, akkor nyerünk ugyan két különböző

B_{1}

és

B_{2}

pontot, de

C_{1} = C_{2} = A

, vagyis az

e

egyenes mindkét esetben a

b

oldallá fajul és megoldásról nem beszélhetünk. Minden más esetben a megoldások száma:

2

. Ha csak azt az

e

egyenest tekintjük megoldásnak, amely a háromszöget nem az oldalak meghosszabbításában metszi, akkor egy ilyen szorosabb értelemben vett megoldás létezésének szükséges és elégséges hogy

α < 90^{\circ}

, és amellett

\frac{α}{2} < β

. Ugyanis, ha

α > 90^{\circ}

, akkor a

C_{1}

pont nem kerülhet az

A B

szakaszra, ha pedig

90^{\circ} > α

, de

45^{\circ} > \frac{α}{2} > β

, akkor a

B_{1}

pont nem kerülhet az

A C

szakaszra.

II. megoldás: Rajzolunk a keresett törtvonalhoz hasonló

A B^{*} C^{*} D_{1}^{*}

, ill.

A B^{*} C^{*} D_{2}^{*}

törtvonalakat (2. ábra).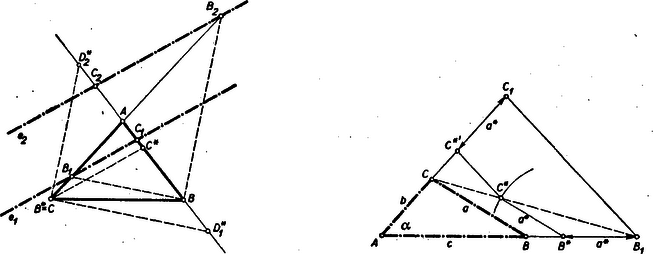

2. ábra

Az egyszerűség kedvéért legyen

B^{*} = C

. E törtvonalakat az

A

pontból, mint hasonlósági centrumból kicsinyítve vagy nagyítva úgy, hogy

D_{1}^{*}

ill.

D_{2}^{*}

B

pontba kerüljön, nyerjük a két megoldást.
Mivel

C^{*} D_{1}^{*} = C^{*} D_{2}^{*} = C^{*} B^{*}

, azért a

D_{1}^{*}

B^{*}

D_{2}^{*}

pontok a

C

középpontú körön fekszenek és így ‐ a Thales-tétel értelmében

B^{*} D_{1}^{*} ⊥ B^{*} D_{2}^{*}

. A

B

ponton át ez utóbbi ket egyenessel húzott párhuzamosak metszik ki az

A C

egyenesből a keresett

B_{1}

ill.

B_{2}

pontokat. A taglalás ugyanahhoz az eredményhez vezet, mint az első megoldásban.