Feladat: 147. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Csiszár I. ,  Daróczy A. ,  Farkas L. ,  Fekete J. ,  Fodor Mária ,  Golla Gy. ,  Gulácsy Sára ,  Harza T. ,  Jakubovics J. ,  Kardos Erzsébet ,  Katz T. ,  Koltai H. ,  Makkai M. ,  Orlik P. ,  Perneczky L. ,  Rázga T. ,  Szabados J. ,  Szeidl Béla ,  Udvari A. ,  Zsombok Z. 
Füzet: 1954/március, 86 - 87. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1953/szeptember: 147. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ABC hegyesszögű háromszögben az AB oldal, mint átmérő fölé rajzolt Thales-kör átmegy az ma és mb magasságok, A1, ill. B1 talppontjain (1. ábra).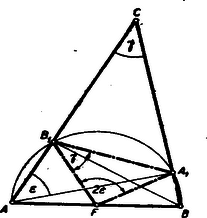

 
 
1. ábra
 

Az AB oldal felezőpontja F a Thales-kör középpontja, tehát az FA1B1▵ tényleg egyenlőszárú, mert FA1=FB1 a Thales-kör sugara. Az A1AB1∢=ε szög az AA1C derékszögű háromszögben γ pótszöge, vagyis ε=90-γ. Másrészt az ε szög a Thales-kör A1B1^ ívén nyugvó kerületi szög, tehát az ugyanezen az íven nyugvó középponti szög: A1FB1∢=2ε=180∘-2γ, és így az FA1B1 egyenlőszárú háromszög alapján nyugvó szögek mindegyike 180∘-(180∘-2γ)2=γ.
A tétel és bizonyítása változatlan, ha az α és β szögek közül valamelyik tompaszög (2. ábra).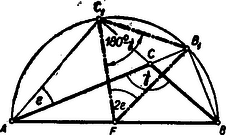
 
 
2. ábra
 

Csak ha a γ szög tompaszög, akkor ε nem a γ-nak, hanem a γ mellékszögének pótszöge (3. ábra), vagyis
ε=90∘-(180∘-γ)=γ-90∘, és az F csúcspontnál levő szög, mint középponti szög egyenlő 2γ-180∘-kal, amiből az alap mellett fekvő szögek 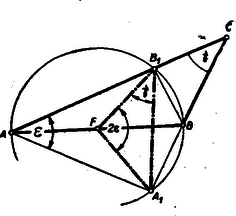180∘-(2γ-180∘)2=180∘-γ.
 
 
3. ábra
 

Ez esetben tehát a tétel úgy módosul, hogy az alapon fekvő szögek a harmadik csúcsnál levő szög kiegészítő szögével egyenlők.
 

Szeidl Béla (Bp., VIII., Apáczai Csere J. g. II. o. t.)
 

Megjegyzés: A feladat általánosítása az 1953. évi Rákosi-verseny II. fordulójára kitűzött 2. feladatnak (l. VII. köt. 1. sz. 1953. szept. 6. old.). Az ott szereplő 60∘-os szög csúcsát O-val jelölve, az ottani A1B1O▵ veszi át az itteni háromszög szerepét. Ugyanis, amint a kérdéses feladat I. megoldásában bizonyítást nyer, hogy A1B⊥OB1 és B1A⊥OA1, így az A1B1 oldal C felezőpontjával alkotott ABC▵ az itt bizonyított tétel szerint egyenlőszárú: AC=BC és az ABC∢=BAC∢=A1OB1∢=60∘, vagyis ABC▵ szabályos. (Az itt általánosított tételben 60∘ helyett γ szerepel.)