Kezdőlap


Feladat:	146. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke Gy. , Csiszár Imre , Kiss Krisztina , Orlik Péter , Rázga Tamás , Udvari A.
Füzet:	1954/február, 46 - 49. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Síkgeometriai szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/szeptember: 146. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Megoldás: Képzeljük a feladatot megoldottnak. Az átlók a négyszög $A ∢$ ill. $B ∢$ -ét $α_{1}$ és $α_{2}$ ill. $β_{1}$ és $β_{2}$ , szögekre osztják oly módon, hogy a $P E$ távolság $A$ -ból $α_{2}$ szög alatt, az $F Q$ távolság pedig $B$ -ből $β ∢$ szög alatt látszik.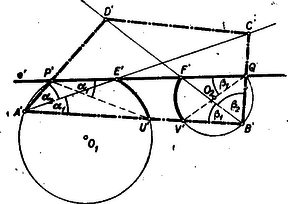

1. ábra

Mivel e szögek a négyszöggel együtt adottak, azért a fentiek alapján könnyen szerkeszthetünk az adott négyszöghöz hasonló

A' B' C' D'

négyszöget valamely

e'

egyenesen tetszőlegesen felvett

P' E' = E' F' = F' Q'

távolságokhoz.
A szerkesztés menete: A

P' E'

és

F' Q'

távolságokhoz megszerkesztjük az

A'

, illetőleg

B'

-pontok mértani helyét, azaz az

α_{2}

, ill.

β_{2}

kerületi szögeknek megfelelő,

O_{1}

ill.

O_{2}

középpontú látóköríveket az

e'

egyenes ugyanazon az oldalán (1 ábra). A keresett

A' B'

egyenes a két látókörívből ‐ az

A'

és

B'

-n kívül ‐ kimetszi az

U'

, ill.

V'

pontokat. Az

E' U'

és

F' V'

körívekhez tartozó kerületi szögek:

α_{1}

, ill.

β_{1}

, adottak, tehát

U'

és

V'

könnyen megszerkeszthetők. Az

U' V'

egyenes metszi ki a két látókörívből második metszéspontként az

A'

és

B'

csúcspontot. Az

A' E'

és

B' F'

egyenesek szolgáltatják az

A' B' C' D'

négyszög átlóit, míg

A' P'

, ill.

B' Q'

lesznek a keresett négyszöghöz hasonló

A' B' C' D'

négyszög oldalainak hordozói. Az így nyert négyszöget (a

P' E' F'

és

Q'

pontokkal együtt) valamilyen hasonlósági centrumból tehetjük a megadott a négyszöggel egybevágóvá.

Orlik Péter (Bp., V., Eötvös g. II. o. t.)

2. ábra

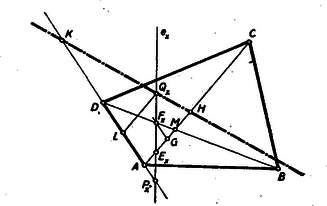II. megoldás: A betűzést a 2. ábra mutatja. Egyelőre tekintsünk el attól, hogy a

Q

pont rajta legyen a

B C

oldalon, hanem határozzuk meg a

Q

pontok mértani helyét, ha az

e

egyenes mozog úgy, hogy a rajta fekvő

P

E

F

pontok az

A D

oldalon, illetőleg az

A C

és

B D

átlókon mozognak olyan módon, hogy mindig

P E = E F = F Q

.
Vegyünk fel az

A C

átlón egy tetszőleges

E_{x}

pontot. Legyen

A E_{x} = x

. Ha

A G = 2 x

és

G

-n át

A D

-vel húzott párhuzamos a

B D

átlót

F_{x}

-ben metszi, akkor az

E_{x} F_{x} = e_{x}

egyenes nyilván olyan

P_{x}

pontban metszi az

A D

oldalt, hogy

P_{x} E_{x} = E_{x} F_{x}

. Az

e_{x}

tehát a mozgó

e

egyenesnek egy ‐ az

x

távolsággal jellemzett ‐ helyzete. Vegyük fel az

e_{x}

-en a

Q_{x}

. pontot úgy, hogy

F_{x} Q_{x} = E_{x} F_{x}

és az

A C

átlón a

H

pontot úgy, hogy

M H = \frac{A M}{2}

. A

Q_{x}

-en át az

A C

átlóval húzott párhuzamos messe az

A D

oldalt

L

-ben, a

Q_{x} H

egyenes pedig ugyancsak az

A D

oldalt

K

-ban. Jelöljük a

K D

távolságot

y

-nal. Fejezzük ki

y

-t az adott távolságokkal. Mivel

A P_{x} E_{x Δ} ≃ G F_{x} E_{x Δ}

, azért

A P_{x} = G F_{x}

, továbbá

G F_{x} : A D = M G : M A

.
Az egyszerűség kedvéért legyen

A D = d

M A = e

, akkor

M G = e - 2 x

, és így

\begin{matrix} G F_{x} = \frac{d (e - 2 x)}{e} . \end{matrix}

Q_{x} L : x = P_{x} Q_{x} : P_{x} E_{x} = 3 : 1, vagyisQ_{x}L=3x

,

továbbá

\begin{matrix} P_{x} L = 3 A P_{x} = 3 G F_{x}, és így A L = 2 G F_{x} = \frac{2 d (e - 2 x)}{e} . \end{matrix}

Végül

\begin{matrix} K L = K A - A L = y + d - \frac{2 d (e - e x)}{z}, \end{matrix}

\begin{matrix} Q_{x} L : A H = K L : K A, \end{matrix}

vagyis

\begin{matrix} 3 x : \frac{3 e}{2} = (y + d - \frac{2 d (e - 2 x)}{e}) : (y + d) . \end{matrix}

Ebből:

\begin{matrix} x y + x d = \frac{e y}{2} + \frac{d e}{2} - d (e - 2 x), \end{matrix}

azaz

\begin{matrix} y (x - \frac{e}{2}) = 2 d x - d e + \frac{d e}{2} - d x = d (x - \frac{e}{2}), \end{matrix}

és így

\begin{matrix} y = d, \end{matrix}

Tehát

y

(és ezzel a

K

pont helyzete) független

x

-től, vagyis a

H Q_{x}

, egyenesek állandóan átmennek a szilárd

K

ponton, és mivel a

H

pont is szilárd, azért a

Q_{x}

pontok mértani helye a

H K

egyenes.
A szerkesztés menete: Megszerkesztjük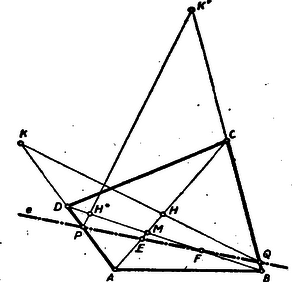

D K = A D

és

M H = \frac{A M}{2}

alapján a

K

és

H

pontokat (3. ábra).

3. ábra

K H

egyenes metszi ki a

B C

oldalból a keresett

Q

pontot. Hasonlóképpen megszerkesztve

C K^{*} = B C

és

M H^{*} = \frac{B M}{2}

alapján a

K^{*}

és

H^{*}

pontokat, a

K^{*} H^{*}

egyenes és az

A D

oldal metszéspontja szolgáltatja a keresett

P

pontot.

Csiszár Imre (Bp., I., Petőfi g. II. o. t.)

III. megoldás: Képzeljük a feladatot megoldottnak és toljuk el az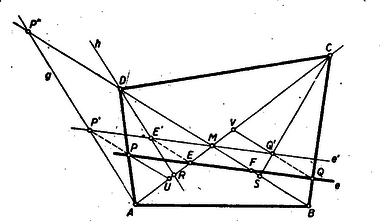

e

egyenest önmagával párhuzamosan a

B D

átló mentén, amíg az

F

pont

M

-be, az

e

egyenes

e'

-be kerül (4. ábra).

4. ábra

Akkor a

Q

E

és

P

pontok

Q'

E'

P'

-be kerülnek és messe a

P P'

és

Q Q'

A C

átlót az

U

, ill.

V

pontban.
Mivel

M E E'_{Δ} ≃ E U P_{Δ}

, azért

U P = E E' = P P'

.
Ha

U

A C

átlón,

P

A D

oldalon mozog úgy, hogy

U P ∥ B D

mindig fennáll, akkor a

P'

pont leírja az

A P' = g

egyenest. Ugyanakkor az

M P' = e'

egyenes

M

körül forog és az

M P'

távolság

E'

felezőpontja leírja a

g

egyenessel párhuzamos

h

egyenest. Ha

P

g

egyenesen való mozgása közben eléri a

g

és

B D

metszéspontját,

P''

-t, akkor a

P

pont (az

A D

oldalon)

D

-be ér, az

U

pont pedig (az

A C

átlón)

M

-be kerül. Tehát

M D = D P''

, amiből következik, hogy az

M P'

távolság felezőpontja

E'

h

egyénesen mozogva) is

D

-be kerül. Ha

P'

mozgása közben (

U

-val és

P

-vel együtt)

A

-ba kerül, akkor

E'

nyilván az

A M

távolság

R

felezőpontjában lesz. Tehát az

E'

pont pályája, a

h

egyenes nem más, mint az

R D

egyenes, amely tehát könnyen megszerkeszthető.
Hasonlóképpen mivel

M E E'_{Δ} ≃ M V Q'_{Δ}

azért

V Q' = E E' = Q Q'

, amiből következik, hogy ha

Q

végighalad a

C B

oldalon és

V

C A

átlón, úgy, hogy

V Q ∥ B D

állandóan fennáll, akkor

Q'

leírja a

C S

egyenest, ahol

S

B M

távolság felezőpontja.
A szerkesztés menete: Megszerkesztve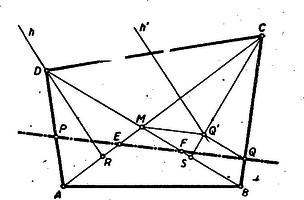

E'

és

Q'

mértani helyét, amelyek ‐ amint láttuk ‐ nem mások, mint az

A M D_{Δ}

, ill.

B M C_{Δ}

-nek

D R

, ill.

C S

súlyvonala, már csak az marad hátra, hogy

C S

-n

Q'

-t úgy határozzuk meg, hogy

Q' M = M E'

legyen. E célból a

D R = h

egyenesnek megszerkesztjük az

M

pontra nézve a

h'

tükörképét, amely kimetszi a

C S

egyenesből a keresett

Q'

pontot.

Q'

-n át

B D

-vel húzott párhuzamos metszi ki a

B C

oldalon a keresett

Q

pontot, amelyen át

Q' M

-mel húzott párhuzamos a keresett

e

egyenes (5. ábra).

5. ábra

Rázga Tamás (Bp., II., Rákóczi g. II. o. t.)