Kezdőlap


Feladat:	137. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh J. , Beke Éva és Mária , Beleznay F. , Biczó Géza , Edöcsény L. , Harza Tibor , Komjátszegi L. , Krammer G. , Orosz Á. , Pátkai Gy. , Quittner P. , Szendrei I. , Tóth Ágota , Uray Z.
Füzet:	1954/január, 9 - 11. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1953/május: 137. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen a keresett $A B C_{△}$ adott súlyvonala $A A_{1} = s_{a}$ . Az $A B A_{1 △}$ és az $A C A_{1 △}$ köré írt körök adott $r_{1}$ és $r_{2}$ sugarai $s_{a}$ -val együtt $(r_{2} \geq r_{1} \geq \frac{s_{a}}{2})$ meghatározzák ‐ mint kerületi szögeket ‐ a keresett $A B C_{△}$ háromszög $β$ , ill. $γ$ szögét. Ha feltesszük, hogy $r_{1} < r_{2}$ , akkor $β > γ$ és így $180^{\circ} - β$ és $γ$ is megfelelnek feltételeinknek, mert $180^{\circ} - β + γ < 180^{\circ}$ . ( $180^{\circ} - γ$ és $β$ nem felel meg, mert e két szög összege $180^{\circ} + β - γ > 180^{\circ}$ .) Tehát ha $β$ és $γ$ -val, ill. $180^{\circ} - β$ és $γ$ -val háromszögeket szerkesztünk, akkor a keresett $A B C_{△}$ -höz hasonló háromszöget kapunk. Ezeket az adott $s_{a}$ -nak megfelelően nagyítva, ill. kicsinyítve nyerjük a 2 megoldást. Általában $(r_{2} > r_{1} > \frac{s_{a}}{2})$ mindig két megoldás van. Ha $r_{1} = \frac{s_{a}}{2}$ , vagyis, ha $β = 90^{\circ}$ , akkor a két megoldás egybeesik. Ugyancsak egy megoldás van (mégpedig egyenlő szárú), ha $r_{1} = r_{2} > \frac{s_{a}}{2}$ , $r_{1} = r_{2} = \frac{s_{a}}{2}$ esetén pedig a háromszögek egyenessé fajulnak, tehát tulajdonképpen megoldás nincs.

Biczó Géza (Bp., Rákóczi g. II. o. t.)

II. megoldás: Rajzoljuk meg az

A A_{1} = s_{a}

súlyvonal, mint húr fölé az

r_{1}

és

r_{2}

sugarú köröket, amelyeknek középpontja

K_{1}

és

K_{2}

(1. 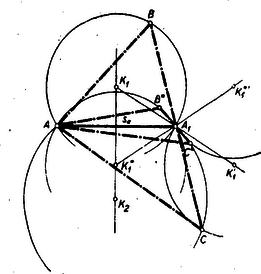ábra).

1. ábra

Feladatunk most már így fogalmazható: az

A_{1}

ponton át olyan szelőt kell meghatározni, amely a két körből egyenlő hosszúságú húrokat metsz ki. Ez a feladat azonban (mint az a tananyagból ismeretes) az egyik körnek az

A_{1}

ponton át való centrális tükrözésével oldható meg.
Két megoldást kapunk aszerint, amint a körközéppontokat a közös húr különböző oldalán (

K_{1}

és

K_{2}

) vagy ugyanazon oldalán (

K_{1}^{*}

és

K_{2}

) vesszük fel.

Harza Tibor (Székesfehérvár, József Attila g. I. o. t.)

III. megoldás: Tekintsük a feladatot megoldottnak (2. ábra).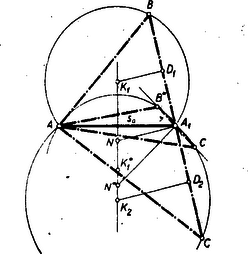

2. ábra

Jelöljük az

A_{1} B

és

A_{1} C

felezőpontjait

D_{1}

ill.

D_{2}

-vel, akkor a feltételünk szerint

\begin{matrix} D_{1} A_{1} = D_{2} A_{1}, \end{matrix}

továbbá

\begin{matrix} D_{1} K_{1} ⊥ B C és D_{2} K_{2} ⊥ B C, \end{matrix}

mert a húrfelező pont és körközéppont összekötése merőleges a húrra. Tehát

D_{1} D_{2}

tulajdonképpen a

K_{1} K_{2}

távolságnak merőleges vetülete a

B C

egyenesen és így a

D_{1} D_{2}

felezőpontjában,

A_{1}

-ben a

B C

-re emelt merőleges egyenes felezi a

K_{1} K_{2}

távolságot, vagyis ‐

K_{1} K_{2}

felezőpontját

N

-nel jelölve

\begin{matrix} N A_{1} ⊥ B C . \end{matrix}

Eszerint a szerkesztés menete: Megrajzoljuk az

s_{a} = A A_{1}

fölé a

K_{1}

és

K_{2}

középpontú

r_{1}

ill.

r_{2}

sugarú köröket,

K_{1} K_{2}

felezőpontját,

N

-et összekötjük

A_{1}

-gyel (2. ábra). Az

A_{1}

-en át

N A_{1}

-re húzott merőleges metszi ki a két körből a

B

és

C

háromszögcsúcsokat. Ugyanez áll természetesen a

K_{1}^{*} K_{2}

-re is.

Megjegyzés: Még mindig vannak számosan, akik a

≫

különböző helyzet

≪

-ekben szerkesztett egybevágó háromszögeket külön megoldásnak tekintik. Jegyezzük meg: Ha csak alakra és nagyságra (tehát nem

≫

helyzet

≪

-re) keresünk háromszöget, akkor csak a nem egybevágó háromszögek számítanak 1 ‐ 1 külön megoldásnak.