Kezdőlap


Feladat:	93. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bakó László , Balogh J. , Bártfai P. , Beleznay F. , Biczó G. , Boros P. , Csiszár I. , Deseő Katalin , Edőcsény L. , Gödény I. , Kálmán Gy. , Kása I. , Krakóczki F. , Krammer G. , Lackner Györgyi , Makai I. , Orosz A. , Orosz Á. , Pátkai Gy. , Perniczky L. , Quittner P. , Szendrei I. , Szentai E. , Szerb Márta , Tanyi T. , Török Ferenc , Váli G.
Füzet:	1953/október, 44 - 45. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek hasonlósága, Síkidomok átdarabolása, Terület, felszín, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1952/december: 93. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A betűzést az 1. ábra mutatja. Jelöljük az adott $A B C D$ négyszög területét $T$ -vel. Az $A P M S$ négyszög nem egyéb, mint az $A B C D$ négyszögnek $2 : 1$ arányú kicsinyítése az $A$ pontból, mint külső hasonlósági centrumból így területe $t_{A P M S} = \frac{T}{4}$ . De $t_{A P M S} = t_{A P O S}$ , mivel az $A P S ▵$ mindkét négyszögnek közös része és

\begin{matrix} t_{S P M} = t_{S P O}, \end{matrix}

mert a közös

S P

oldalhoz tartozó magasságok egyenlők, mivel

M O | | B D | | S P

. Tehát

t_{A P O S} = \frac{T}{4}

. Ugyanez kimutatható, hasonlóképpen a többi 3 résznégyszögre nézve is, és így tételünket bebizonyítottuk.

Török Ferenc (Bp., VI. Kölcsey g. II. o. t.)

1. ábra 2. ábra

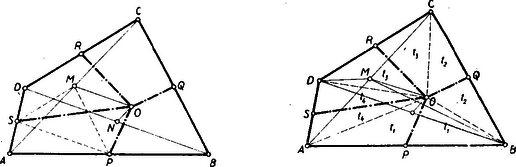II. megoldás: Mivel

B M

és

D M

súlyvonalak felezik az

A C B ▵

ill.

A C D ▵

területét (2. ábra), azért a

B M D

törtvonal felezi az

A B C D

négyszög területét vagyis

\begin{matrix} t_{A B M D} = t_{D M B C} = \frac{T}{2} . \end{matrix}

t_{A B M D}

nem változik, ha az

M

pontot a

B D

átlóval párhuzamosan eltoljuk

O

-ba, vagyis

\begin{matrix} t_{A B O D} = t_{D O B C} = \frac{T}{2}, \end{matrix}

(1)

és hasonlóképpen

\begin{matrix} t_{A B C O} = t_{A O C D} = \frac{T}{2} . \end{matrix}

(2)

O P

O Q

O R

O S

súlyvonalak rendre felezik az

A B O ▵

B C O ▵

C D O ▵

és

D A O ▵

területét. Jelölhetjük az így keletkezett részháromszögek területét rendre

t_{1}

t_{2}

t_{3}

- és

t_{4}

-gyel.
Elég bebizonyítani, hogy

t_{1} = t_{3}

és

t_{2} = t_{4}

, mert ebből már következik, hogy

t_{1} + t_{2} = t_{2} + t_{3} = t_{3} + t_{4} = t_{4} + t_{1}

, vagyis, hogy bármely két szóbanforgó résznégyszög egyenlő.

\begin{matrix} (1) alapján 2 t_{1} + 2 t_{4} & = 2 t_{2} + 2 t_{3}, & (3) \\ (2) alapján 2 t_{1} + 2 t_{2} & = 2 t_{3} + 2 t_{4} . & (4) \end{matrix}

(3) és (4) összeadásából

\begin{matrix} 4 t_{1} + 2 (t_{2} + t_{4}) = 4 t_{3} + 2 (t_{2} + t_{4}), \end{matrix}

vagyis

\begin{matrix} t_{1} = t_{3} . \end{matrix}

(3) vagy (4)-ben

t_{3}

helyébe

t_{1}

-et írva, nyerjük, hogy

\begin{matrix} t_{2} = t_{4} . \end{matrix}

Bakó László (Debrecen, Ref. g. II. o. t.)