Kezdőlap


Feladat:	92. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Almási L. , Aujeszky Géza , Bakó L. , Balogh J. , Bártfai P. , Bauer P. , Beke Éva , Beke Gyula , Beke Mária , Beleznay F. , Berár I. , Béres I. , Biczó G. , Biszterszky Sára , Boros P. , Csiszár I. , Csomos S. , Czili Gy. , Deseő Katalin , Fróna Erzsébet , Gecse Klára , Gulácsy Sára , Harza T. , Ivanyos A. , Jármay Erzsébet , Jermi Gy. , Kálmán Gy. , Kása I. , Kertész Á. , Kiss P. , Kovács István , Krakóczki F. , Krammer G. , Kulcsár Zsuzsa , Lábos E. , Lackner Györgyi , Madari I. , Nagy S. , Németh László , Orlik P. , Orosz A. , Orosz Á. , Pallagi I. , Pasitka B. , Pátkai Gy. , Pázmándy Gy. , Perneczky L. , Quittner P. , Roboz Ágnes , Rozgonyi E. , Szélba L. , Szendrei I. , Szentai E. , Szerb Mária , Szlanka I. , Takács J. , Takács T. , Tanyi T. , Tasnádi Gy. , Tóth L. , Török F. , Ujszászi J. , Uray L. , Várnai I. , Világhy T. , Viola L. , Weiling K.
Füzet:	1953/október, 42 - 44. oldal		PDF \| MathML
Témakör(ök):	Diszkusszió, Háromszögek szerkesztése, Körérintési szerkesztések, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1952/december: 92. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük a feladatot megoldottnak. A betűzést az 1. ábra mutatja.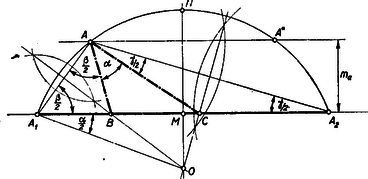

1. ábra

Ha a

B C = a

oldalt

B

-n túl a

B A_{1} = B A = c

oldallal és

C

-n túl

C A_{2} = C A = b

oldallal meghosszabbítjuk, akkor az

A_{1} B A

és az

A_{2} C A

egyenlőszárú háromszögekben az alap mellett fekvő szögek

\frac{β}{2}

ill.

\frac{γ}{2}

, mert két belső szög összege egyenlő a szemközt fekvő külső szöggel. Az

A_{1} A A_{2} ▵

-ben tehát az

A_{1} A_{2}

oldal a háromszög kerülete és az

A ∢ = α + \frac{β}{2} + \frac{γ}{2} = \frac{2 α + β + γ}{2} = \frac{180^{\circ} + α}{2} = 90^{\circ} + \frac{α}{2}

. Tehát az

A

pont egyrészt rajta van az

A_{1} A_{2} = k

fölé rajzolt olyan látóköríven, melynek pontjaiból az

A_{1} A_{2}

szakasz

90^{\circ} + \frac{α}{2}

szög alatt látszik, másrészt rajta van az

A_{1} A_{2}

egyenessel párhuzamos és tőle

m_{a}

távolságban lévő azon egyenesen, amely

A_{1} A_{2}

-nek ugyanazon az oldalán fekszik mint a látókörív.
A szerkesztés menete tehát: Felvesszük az

A_{1} A_{2} = k

távolságot. Megszerkesztjük a fenti két mértani helyet. Ezek metszéspontja

A

(és

A^{*}

) a keresett háromszög egyik csúcspontja. Az

A A_{1}

és

A A_{2}

szakaszokat merőlegesen felező egyenesek metszik ki az

A_{1} A_{2}

távolságból a háromszög

B

és

C

csúcspontjait. Csak egy megoldás van, mert

A^{*}

az előbbi megoldás tükörképét szolgáltatja az

A_{1} A_{2}

távolságot merőlegesen felező egyenesre nézve.
A megoldhatóság feltétele, hogy

\begin{matrix} m_{a} \leq M N = O N - O M = O A_{1} - O M = \frac{A_{1} M}{cos \frac{α}{2}} - A_{1} M tg \frac{α}{2} = \frac{k}{2 cos \frac{α}{2}} - \frac{k sin \frac{α}{2}}{2 cos \frac{α}{2}} = \frac{k}{2} \cdot \frac{1 - sin \frac{α}{2}}{cos \frac{α}{2}} . \end{matrix}

Egyenlőség esetén egyenlőszárú háromszöget nyerünk.

Aujeszky Géza (Bp. II., Rákóczi g. II. o. t.)

II. megoldás: Ismeretes, hogy a háromszöghöz írt körnek az oldalak meghosszabbításán fekvő érintési pontjai az érintők metszéspontjától félkerület távolságban vannak. Ezt felhasználva a szerkesztés menete a következő: Az adott

α

szög szárai között olyan kört szerkesztünk, amely az

A

csúcsponttól

\frac{k}{2}

távolságban fekvő

E_{1}

és

E_{2}

pontokban érinti a szárakat (2. ábra).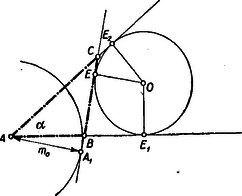

2. ábra

A

körül

m_{a}

sugárral rajzolt kör és az előbbi kör egyik közös belső érintője (érintési pontok

A_{1}

és

E

) metszi ki a szárakból a keresett háromszög

B

és

C

csúcspontjait. Valóban az így nyert háromszög kielégíti feltételeinket: A háromszög kerülete

A B + B E + E C + C A = A B + B E_{1} + E_{2} C + C A = A E_{1} + A E_{2} = \frac{k}{2} + \frac{k}{2} = k

és a

B C = a

oldalhoz tartozó magasság

A A_{1} = m

.
A megoldhatóság feltétele, hogy a két kör ne messe egymást két különböző pontban, vagyis, hogy

m_{a} \leq A O - O E_{1} = \frac{k}{2 cos \frac{α}{2}} - \frac{k}{2} tg \frac{α}{2}

stb. mint az I. megoldásban.

Beke Gyula (Hatvan, Bajza József g. I. o. t.)