Feladat: 49. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Balatoni F. ,  Balatoni I. ,  Beke Éva és Mária ,  Biczó G. ,  Földeák M. ,  Gaál I. ,  Grätzer Gy. ,  Holbok S. ,  Huszár k. ,  Kertész Á. ,  Lackner Györgyi ,  Pázmándy Gy. ,  Quittner P. ,  Robogány I. ,  Tomor B. ,  Vigassy József 
Füzet: 1952/december, 142 - 143. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Szabályos sokszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1952/május: 49. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Szerkesszünk egy tetszőleges sugarú körbe szabályos ötszöget és ezt a kívánt arányban felnagyítjuk ill. kicsinyítjük. (1. ábra)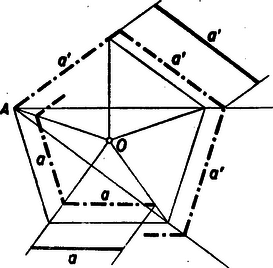

 
 
1. ábra
 

A hasonlósági transzformáció centrumául választhatjuk az ötszög középpontját vagy egyik csúcspontját.
Ez az eljárás lényegében ugyanaz, mint amikor 36∘, 72∘ vagy 108∘-os szöget szerkesztünk.
Nem szerkesztés ‐ természetesen ‐ a szögek lemérése szögmérőről.
 

Vigassy József (Bp. I., Petőfi g. II. o. t.)

 

II. megoldás: A szabályos ötszög egy AB oldala a szemközt fekvő D csúcsponttal egyenlő szárú háromszöget alkot, amelynek alapja az AB=a ötszögoldal, szára az ötszög átlója d, a csúcsnál lévő szöge (mint kerületi szög) 72∘2=36∘ és így az alap melletti szögek 72∘-úak (2. áb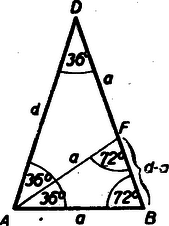ra).
 
 
2. ábra
 

Az alapnál lévő A∢ felező egyenese messe a BD átlót egy F pontban.
A szemközti szögek egyenlősége miatt AB=AF=FD=a és a szögek egyenlősége miatt, ABD▵∼BFA▵.
Tehát FB=d-a és továbbá
(d-a):a=a:d,
vagyis az F pont a BD átlót az aranymetszés szerint osztja.
Ennek alapján az adott a oldalból a d átló elegánsan megszerkeszthető. A szerkesztést a 3. ábra mutatja.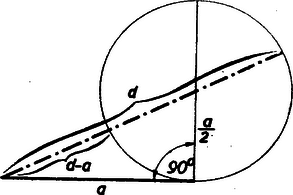
 
 
3. ábra
 

Az a oldal és a d átló ismeretében a szab. ötszög megszerkesztése már triviális.