Kezdőlap


Feladat:	33. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balatoni I. , Biczó G. , Dezső Zoltán , Kovács László , Marik M. , Németh Lehel , Schmidt E.
Füzet:	1952/november, 117 - 119. oldal		PDF \| MathML
Témakör(ök):	Egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1952/április: 33. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük az adott kör középpontját $O$ -val, az adott egyenest $e$ -vel és az $e$ -n tetszőlegesen felvett pontot $P$ -vel. Szerkesszük meg a körhöz az adott $e$ -vel párhuzamos $e_{1}$ és $e_{2}$ érintőket (1. ábra)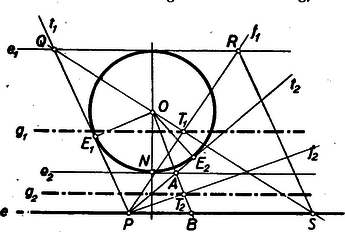

1. ábra

P

-ből a körhöz húzott

t_{1}

érintő messe

e_{1}

-et

Q

-ban, az

e

és

t_{1}

szögfelezője

f_{1}

pedig messe

e_{1}

-et

R

-ben. A

P Q R

nyilván egyenlő szárú, mert az

e

és

f_{1}

szöge, mint váltószög egyenlő az

f_{1}

és

e_{1}

által bezárt szöggel. A

Q O

egyenes felezi a

Q

-ból kiinduló két érintő:

t_{1}

és

e_{1}

szögét és mint ilyen szükségképpen merőleges és felezi a

P R

alapot. Ha a

Q O

egyenes és

e

metszéspontját

S

-sel jelöljük, akkor a

P Q R S

négyszög az előbbiek alapján rombusz. Az

O

-ből az

f_{1}

-re bocsátott merőleges eszerint egyezik a

Q S

rombuszátlóval és e merőlegesnek

T_{1}

talppontja

f_{1}

-en pedig azonos a rombusz átlóinak metszéspontjával. Ha

P

mozog az

e

egyenesen, akkor a rombusz változik, de a

P S

, ill.

Q R

rombuszoldalak mindig az

e

, ilL

e_{1}

egyeneseken maradnak és így a két átló metszéspontja

T_{1}

e

és

e_{1}

párhuzamos egyenesek közét felező

g_{1}

egyenesen mozog. Szóról-szóra ugyanúgy kimutathatjuk ‐ a

t_{2}

érintőt tekintve ‐, hogy a

T_{2}

pontok rajta vannak azon a

g_{2}

egyenesen, amely az

e

és

e_{2}

párhuzamos egyenesek közét felezi. A teljes mértani helyet:

g_{1}

és

g_{2}

(végtelen hosszú) egyeneseket, csak akkor kapjuk, ha a másik két szögfelezőt is figyelembe vesszük.

Deseő Zoltán (Bp. V. Berzsenyi g. II. o. t.)

II. megoldás: Jelöljük

t_{2}

érintési pontját

E_{2}

-vel. Az

O

-ből az

e

-re bocsátott merőleges messe a kört

N

-ben. az

O

-ból az

f_{2}

-re bocsátott merőleges talppontja

f_{2}

-n

T_{2}

; ennek a merőlegesnek metszéspontjai

t_{2}

-vel,

e

-vel legyenek

A

ill.

B

(1. ábra). A merőleges szárú szögek tétele alapján az

N O A ∢ = e f_{2} ∢ = f_{2} t_{2} ∢ = E_{2} O A ∢

és így az

A N O_{▵} ≃ A E_{2} O_{▵}

, mert

O N = O E

és az

O A

oldal közös. De az

A E_{2} O_{▵}

derékszögű (mert a

t

érintő merőleges az

O E

sugárra) és így az

A N O_{▵}

is derékszögű, tehát

A N ⊥ O N

, vagyis

A N ∥ e

. Ez azt jelenti, hogy ha

P

mozog az

e

-n, az

A

befutja az

e_{2}

egyenest, a

B

e

egyenest, és

A B

felezőpontja

T_{2}

befutja az

e_{2}

és

e

párhuzamos egyenesek közét felező

g_{2}

egyenest.

Kovács László (Debrecen, Ref. g. II. o. t.)

III. megoldás: A betűzést a 2. ábra mutatja.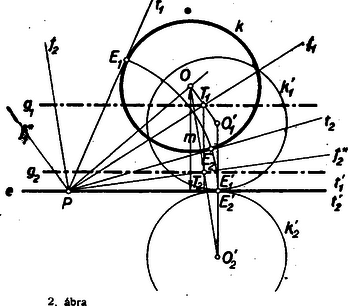

Tükrözzük az adott

k

kört és a

t_{1}

, ill.

t_{2}

érintőket az

f_{1}

, ill.

f_{2}^{*}

szögfelezőkre nézve, akkor az

O

tükörképe

O'_{1}

, ill.

O'_{2}

, a

t_{1}

és

t_{2}

tükörképei egybeesnek

e

-vel, úgyszintén egybeesnek

E_{1}

és

E_{2}

érintési pontok tükörképei az

e

egyenesen és ebben az

E'_{1} \equiv E'_{2}

pontban érintik az adott

k

kör tükörképei:

k'_{1}

és

k'_{2}

e

egyenest.
Ha

P

mozog az

e

egyenesen az

O'_{1}

és

O'_{2}

pontok mozognak az

e

-vel párhuzamos,

e

-től

r

távolságban levő egyeneseken, ha

r

-rel jelöljük az adott kör sugarát. Ha az

O

pontnak az

e

-től való távolságát

m

-mel jelöljük, akkor az

O O'_{1}

és

O O'_{2}

távolságok felezőpontjai:

T_{1}

és

T_{2}

is az

e

-vel párhuzamos

g_{1}

és

g_{2}

egyeneseken mozognak, amelyeknek távolságai

e

-től:

\begin{matrix} \frac{m + r}{2} ill. \frac{m + t}{2} - r = \frac{m - r}{2} . \end{matrix}

(Ez az eredmény másképpen fejezi ki az I. és II. megoldásban megállapított tényt.)