Feladat: 10. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bárdos A. ,  Bujdosó A. ,  Deseő Z. ,  Fülöp J. ,  Huszár k. ,  Kézdy Pál ,  Kozma Vera ,  Lackner Györgyi ,  Németh István ,  Tahy P. 
Füzet: 1952/szeptember, 22 - 24. oldal  PDF  |  MathML 
Témakör(ök): Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):Feladatok: 1952/február: 10. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Képzeljük el a feladatot megoldottnak és rajzoljuk meg a háromszög köré írt kört. (1. ábra.)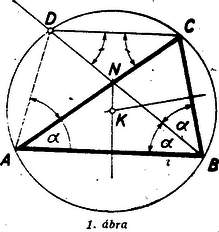

 

Messe a β szög felezője e kört D-ben és az AC=b oldalt N-ben. A kerületi szögek tétele szerint AD=DC=BC=a mert e három húrhoz tartozó körívek mindegyike α kerületi szöget határoz meg. Az ABCD trapéz tehát egyenlő szárú és a fenti oldalakon kívül ismerjük még az AC=BD átlót. Ezen adatokból e trapéz és vele együtt keresett háromszög könnyen megszerkeszthető, feltéve, hogy az ABC▵(≅BCD▵) egyáltalán szerkeszthető, vagyis feltéve, hogy a+a>b, azaz a>b/2. Másrészt mivel α<β azért a<b és így a megoldhatóság feltétele:
b2<a<b.
 

Németh István (Bp. V., Piarista g. II. o. t.)

 

II. megoldás: Bebizonyítjuk (körülírt kör nélkül), hogy az α szög nem más, mint egy b alapú és a szárú egyenlő szárú háromszögnek az alap melletti szöge, mely mint olyan, könnyen szerkeszthető. Ez a bizonyítás ismét többféleképpen történhetik.
a) Képzeljük ismét a feladatot megoldottnak (1. ábra). A C csúcsponton át húzzunk az AB oldallal párhuzamos egyenest. A β szög felezője messe ezt a párhuzamos egyenest D-ben és az AC oldalt N-ben. A C és D pontoknál keletkezett, vonalkázott ívvel jelölt, két szög külön-külön, mint váltószög egyenlő α-val. Tehát a BCD, CND és ANB háromszögek egyenlő szárúak, vagyis CD=BC=a és CD=BN+ND=AN+NC=AC=b.
b) Ismét a megszerkesztendő háromszögből kiindulva, tükrözzük a C ponthoz tartozó mc magasság körül pl. az a oldalt (2. ábra.).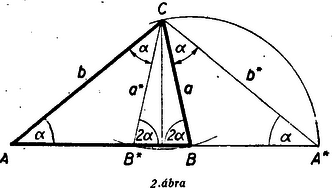
 
 
2. ábra
 

B és a tükörképe B*, ill. a*, és így a=a* lévén a BCB* egyenlő szárú háromszögben mindkét alap mellett fekvő szög 2α. A keletkezett AB*C▵-ben az A-nál fekvő szög α, a B*-nál fekvő külső szög az előbbiek szerint 2α, tehát a C-nél lévő szög ‐ a külső szögek tétele szerint ‐ szintén α, vagyis AB*=B*C=a.
Hasonló eredményre jutunk, ha a nagyobbik, b oldalt tükrözzük.
Itt még azt is látjuk, hogy az adott a és b oldalakból megszerkesztve az AB*C egyenlő szárú háromszöget, a B*-nak az mc magasságra vonatkoztatott tükörképe B adja az A és C pontokkal együtt a megoldást.
c) Ha a rövidebb a oldalt lemérem B-ből az AB oldal meghosszabbításaként, vagyis BA*=BC=a, akkor az A*BC egyenlő szárú háromszögben az A* és C-nél fekvő szögek külön-külön α-val egyenlők, mert hiszen a B-nél lévő külső szög 2α. Az A*CA▵ tehát egyenlő szárú és így A*C=b.
A megoldhatóság feltétele azonos az I. megoldásnál nyert feltétellel.
 

Kézdy Pál (Bp. II., Rákóczi g. II. o. t.)

 

III. megoldás: Húzzuk meg az elképzelt megoldásban (1. ábra) a β szög felezőjét, a BN távolságot. A BNC∢, mint az ABN▵ külső szöge egyenlő 2α-val, és így BNC▵∼ABC▵, vagyis AC:BC=BC:NC, azaz b:a=a:NC, miből NC, mint negyedik arányos, könnyen megszerkeszthető.
A megoldhatóság feltétele, hogy a BCN▵ szerkeszthető legyen. E háromszög oldalai BC=a, NC=a2b és BN=b-a2b. Kell tehát, hogy
b-a2b=b2-a2b<a+a2b=ab+a2b,
vagyis
b2-a2<a(b+a),b-a<a,


miből
b2<a(<b),
ami azonos az eddigiekben nyert feltétellel.
 

IV. megoldás: A sinus-tétel értelmében
ba=sin2αsinα=2sinαcosαsinα=2cosα,
miből
cosα=b2a.
Ennek alapján az α szög mindig szerkeszthető, ha b<2a, vagyis b2<a.
Megjegyzés: Mivel másrészt a<b, azért (cosα a legkisebb, ha a a legnagyobb és fordítva)
12<cosα<1

Tehát 60∘>α>0∘ és 120∘>β>0∘.
 

Nagykanizsai Irányi D. g. Szakköre.