|
| Feladat: |
9. matematika gyakorlat |
Korcsoport: 16-17 |
Nehézségi fok: átlagos |
| Megoldó(k): |
Ágoston Gy. , Avakunovics O. , Balatoni F. , Batha J. , Beke Éva és Mária , Beleznay F. , Bognár P. , Bujdosó A. , Cseh I. , Csernyák L. , Csizek F. , Erős I. , Érsek L. , Farkasfalvy M. , Fogarassy Anna , Földeák M. , Földi L. , Grätzer Gy. , Gyovai E. , Gömöri P. , Hangay Gy. , Huszár k. , Illényi T. , Kállai T. , Kiss Piroska , Kollár L. , Kovács L. , Kozma Vera , Krammer G. , Kristóf T. , Lackner Györgyi , Ladányi J. , Lászlóffy A. , Miskovszky Gy. , Mohos B. , Molnár Zsuzsanna , Nagy E. , Németh I. , Németh L. , Poll M. , Quittner P. , Rácz M. , Radnai J. , Reichlin V. , Roboz Ágnes , Rosenblüth Erzsébet , Sántha E. , Schuder J. , Skrinyár M. , Sohár P. , Szabó I. , Szélba L. , Szendrei I. , Szepesi J. , Szlankai I. , Sztranhura Valéria , Tahy P. , Tasnádi G. , Tóka P. , Tomor B. , Turza S. , Várnai I. , Völgyesi A. , Zarka S. |
| Füzet: |
1952/szeptember,
21 - 22. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Diszkusszió, Síkgeometriai szerkesztések, Gyakorlat |
| Hivatkozás(ok): | Feladatok: 1952/február: 9. matematika gyakorlat |
|
|
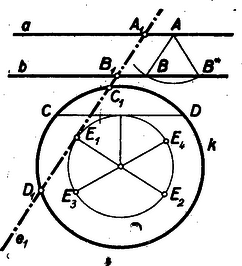
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az egyenes tetszőleges pontjából sugárral rajzolt körív kimetszi a egyenesből a és pontokat. Az és egyenesek szolgáltatják a keresett egyenes irányát.
Az adott körben felveszünk egy tetszőleges helyzetű hosszúságú húrt. E húrt érintő koncentrikus körhöz szerkesztünk a már megszerkesztett két iránnyal párhuzamos érintőket, vagyis a kör középpontjából merőlegeseket húzunk a két irányra; e merőlegesek metszik ki a koncentrikus körből az , , és pontokat. ( és ‐ az ábrán a négy megoldás csak egyike van feltüntetve.)
Az és egyenesek távolságát -vel, az adott kör sugarát -rel jelölve:
| Beke Éva és Mária (Bp. XIII., Épületgépészeti techn. I. o. t.) |
|
|
 PDF
PDF