Kezdőlap


Feladat:	F.3000	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Alács Péter , Bámer Balázs , Bánhalmi András , Bárász Mihály , Becsei András , Birszki Bálint , Burcsi Péter , Draskovits Dénes , Ehreth Imre , Erdélyi László , Erdélyi Máté , Farkas Péter , Fey Dániel , Hegedűs Viktor , Horváth István , Izsák Ferenc , Kasza Tamás , Kiss Zoltán , Kovács Baldvin , Kovács Szabolcs , Maróti Attila , Mosonyi Milán , Nagy Gábor , Németh Ákos , Perényi Márton , Puskás Csaba , Répás Csaba , Szeredi Tibor , Szobonya László , Tejfel Máté , Véber Miklós , Vörös Zoltán
Füzet:	1994/december, 495 - 496. oldal		PDF \| MathML
Témakör(ök):	Téglatest, Paralelepipedon, Térfogat, Tetraéderek, Pitagorasz-tétel alkalmazásai, Feladat
Hivatkozás(ok):	Feladatok: 1994/február: F.3000

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy a tetraéder létezik. Ismeretes, hogy egy tetraéder lapjai akkor és csak akkor egybevágóak, ha a köré írt paralelepipedon téglatest. Ismert tétel az is, hogy ha a tetraéder lapjai egybevágóak, akkor a lapok hegyesszögű háromszögek, továbbá, hogy a tetraéder térfogata a körülírt paralelepipedon térfogatának harmada. Ezek a tételek (bizonyítási útmutatással) megtalálhatók a Geometriai feladatok gyűjtemény I. 2088‐2090., illetve 2083. feladataiként. Mivel a körülírt paralelepipedon téglatest, a tetraéder szemközti élei egyenlők lesznek. Ábránk így készült, amelynek alapján meghatározzuk a paralelepipedon élei hosszát:

\begin{matrix} x^{2} + y^{2} & = c^{2} \\ y^{2} + z^{2} & = b^{2} & (1) \\ z^{2} + x^{2} & = a^{2} . \end{matrix}

(1)-ből

x^{2} + y^{2} + z^{2} = \frac{a^{2} + b^{2} + c^{2}}{2}

, amelybe az (1)-ben szereplő egyenletek jobb oldalát helyettesítve:

\begin{matrix} x = \sqrt[]{\frac{a^{2} - b^{2} + c^{2}}{2}}, y = \sqrt[]{\frac{- a^{2} + b^{2} + c^{2}}{2}}, z = \sqrt[]{\frac{a^{2} + b^{2} - c^{2}}{2}} . \end{matrix}

A paralelepipedon térfogata

x \cdot y \cdot z

, ezért a tetraéder térfogata:

\begin{matrix} V = \frac{1}{3} x \cdot y \cdot z = \frac{1}{6 \cdot \sqrt[]{2}} \cdot \sqrt[]{(- a^{2} + b^{2} + c^{2}) \cdot (a^{2} - b^{2} + c^{2}) \cdot (a^{2} + b^{2} - c^{2})} . \end{matrix}

Mivel a tetraéder lapjai hegyesszögű háromszögek,

\begin{matrix} a^{2} < b^{2} + c^{2} és b^{2} < a^{2} + c^{2} és c^{2} < a^{2} + b^{2}, \end{matrix}

tehát a négyzetgyökjel alatti tényezők pozitívak.

Maróti Attila (Szeged, Ságvári E. Gimn., IV. o. t.) dolgozata alapján

Megjegyzés. A feladat szövege szerint természetesnek vehettük, hogy a tetraéder létezik, és ekkor fennáll a (2) feltétel. Megfordítva megmutatható, hogy ha a (2) fennáll, akkor létezik olyan tetraéder, amelynek lapjai

a

b

c

oldalú egybevágó háromszögek, és egyetlen ilyen tetraéder van.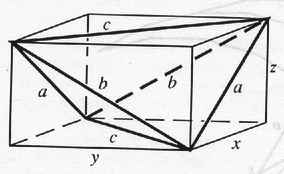