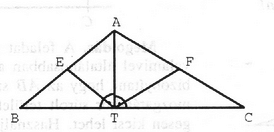
Először belátjuk, hogy bármely háromszög felbontható négy egyenlő szárú háromszögre. Az 1. ábra $AT$ magassága a háromszöget két derékszögű háromszögre bontja. (Ilyen magasság nyilván mindig van.) A $T$ pontot az $AB$, illetve $AC$ oldalak felezőpontjával összekötve négy egyenlő szárú háromszöget kapunk.
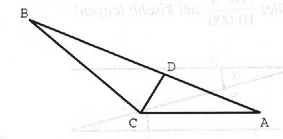
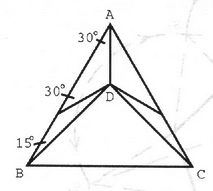
Ezután megmutatjuk, hogy bármely háromszög felbontható öt egyenlő szárú háromszögre. Ha a háromszög nem szabályos, akkor van két különböző hosszúságú oldala, feltehető, hogy $AB>BC$. Mérjük rá $BC$-t az $AB$-re, és legyen $BD=BC$ (2. ábra). A $BCD▵$ egyenlő szárú, és az első esetünk szerint az $ACD▵$ feldarabolható 4 egyenlő szárú háromszögre. A szabályos háromszög 5 egyenlő szárú háromszögre bontását a 3. ábrán láthatjuk, amely úgy készült, hogy $ABD\sphericalangle ={15}^{\circ }$ legyen.
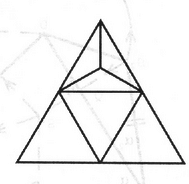
Bebizonyítjuk még, hogy minden háromszög feldarabolható hat egyenlő szárú háromszögre. Ha a háromszög nem szabályos, akkor a 2. ábra szerint járunk el úgy, hogy az $ACD▵$-et a második eset szerint 5 egyenlő számú háromszögre bontjuk. Ha a háromszög szabályos, a 4. ábra szerint daraboljuk fel.
Tegyük fel ezután, hogy egy háromszöget $m$ egyenlő szárú háromszögre bontottunk fel. Ha ekkor az egyik egyenlő szárú háromszöget az első eset szerint 4 egyenlő szárú háromszögre bontjuk, akkor összesen $m+3$ (egyenlő szárú) háromszög lesz. Ezt az eljárást folytatva $m+3k$ egyenlő szárú háromszögre darabolhatjuk a szóban forgó alakzatot, ahol $k$ tetszőleges természetes szám. Mivel $4+3k$ vagy $5+3k$ vagy $6+3k$ alakban minden $n\left(\ge 4\right)$ egész előáll, a feladatot megoldottuk.