Kezdőlap


Feladat:	F.2990	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Abért Krisztián , Bánhalmi András , Becsei András , Benkő Péter , Birszki Bálint , Burcsi Péter , Dévényi Csaba , Erdélyi László , Farkas Illés , Farkas Péter , Fey Dániel , Galácz Ábel , Gémes Tamás , György András , Halász György , Hegedűs Márton , Hertz István , Horváth István , Izsák Ferenc , Juhász Sándor , Kiss Zoltán , Kováts Antal , Nagy Vilmos , Németh Ákos , Németh Zoltán , Puskás Zsolt , Répás Csaba , Sánta Zsuzsa , Séllei Béla , Somogyi Balázs , Szádeczky-Kardoss Szabolcs , Szobonya László , Tóth László , Újváry-Menyhárt Mónika , Valkó Benedek , Véber Miklós
Füzet:	1994/október, 360 - 362. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Körérintési szerkesztések, Inverzió, Apollóniusz-kör, Feladat
Hivatkozás(ok):	Feladatok: 1993/december: F.2990

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat feltételeinek két kör is megfelelhet. Az egyiket az ábrán láthatjuk. A másik az lesz, amelyik a nagyobb körrel és az érintővel közrefogja a kisebb kört. Legyen az adott körök középpontja $O_{1}$ és $O_{2}$ , a sugaruk $R$ és $r$ . A szerkesztendő kör középpontja $O$ , sugara $x$ . Az érintési pontok legyenek $E_{1}$ , $E$ , $E_{2}$ . Húzzunk párhuzamost $E_{2}$ -n át $O_{1} O_{2}$ -vel. A Pitagorasz-tétel szerint

\begin{matrix} E_{1} E_{2}^{2} = {(R + r)}^{2} - {(R - r)}^{2} = R \cdot r, \end{matrix}

tehát

E_{1} E_{2} = 2 \sqrt[]{R \cdot r}

. Hasonlóan

E_{1} E = 2 \sqrt[]{R \cdot x}

E E_{2} = 2 \sqrt[]{r \cdot x}

. Mivel

E_{1} E_{2} = E_{1} E + E E_{2}

, azért

\begin{matrix} 2 \sqrt[]{R \cdot r} = 2 \sqrt[]{R \cdot x} + 2 \sqrt[]{r \cdot x}, \end{matrix}

amiből

\begin{matrix} \sqrt[]{x} = \frac{\sqrt[]{R \cdot r}}{\sqrt[]{R} + \sqrt[]{r}}, azaz x = \frac{R \cdot r}{R + 2 \sqrt[]{R r} + r} . \end{matrix}

Ezt úgy szerkeszthetjük meg, hogy megszerkesztjük

\sqrt[]{R r}

-t, majd a nevezőt, végül

x

-et az

R

és

r

, valamint a nevezőhöz tartozó negyedik arányosként kapjuk.
A másik megoldást az ábra alapján úgy képzelhetjük el, mintha az

O_{2}

és

O

középpontú kör lenne adott, és az

O_{1}

középpontú kört kellene megszerkeszteni. Ha most az

O_{1}

középpontú kör sugarát

R

helyett

x

-szel jelöljük, és a másik két sugár lesz

R

, illetve

r

, akkor (1) így alakul:

\sqrt[]{x \cdot R} = \sqrt[]{x \cdot r} + \sqrt[]{R \cdot r}

, és

x = \frac{R \cdot r}{{(\sqrt[]{R} - \sqrt[]{r})}^{2}}

. A szerkesztés hasonlóan végezhető, mint az első esetben. Azt is láthatjuk, hogy az első eset szerinti megoldás mindig létezik, a másik pontosan akkor, ha

R \neq r

. Ezért a feladatnak egy megoldása van, ha

R = r

, egyébként pedig kettő.

Farkas Péter (Budapest, Szent László Gimn., III. o. t) és
Németh Ákos (Fazekas M. Főv. Gyak, Gimn., IV. o. t.) dolgozata alapján

Megjegyzések. 1. A fenti számításokat Farkas Péter igen elegánsan végezte el annak ismeretében, hogy ha négy kör kölcsönösen érinti egymást, akkor a görbületeik négyzetösszegének kétszerese megegyezik a görbületek összegének négyzetével. Ezt a tételt Descartes fedezte fel, alkalmazása szempontjából a körök között egyenesek is szerepelhetnek zérus görbülettel. Egy

r

sugarú kör görbülete a körvonal minden pontjában

\frac{1}{r}

. A feladatunk általánosítását jelentő problémát, amely az idézett tétel bizonyításához vezet, érdeklődő olvasóink megtalálhatják H. S. M. Coxeter: A geometriák alapjai c. művének 31‐32. oldalán.
2. Németh Ákos inverzióval is megoldotta a feladatot. Az inverzió középpontjául a két kör érintési pontját választotta. Így a két adott kör inverze két párhuzamos egyenes lesz, és a keresett kör(ök) inverzét a két párhuzamos egyenest és a közös érintő inverzkörét érintő kör adja.
Az inverzióról H. S. M. Coxeter‐S. L. Greitzer: Az újra felfedezett geometria c. mű 175‐204. oldalán olvashatnak megoldóink.
3. Feladatunk speciális esete az Apollóniosz-féle feladatnak, amely legáltalánosabban így fogalmazható meg: Három adott körhöz szerkesztendők azok a körök, amelyek az adott körök mindegyikét érintik (a körök között ‐ elfajuló esetként ‐ egyeneseket is megengedve).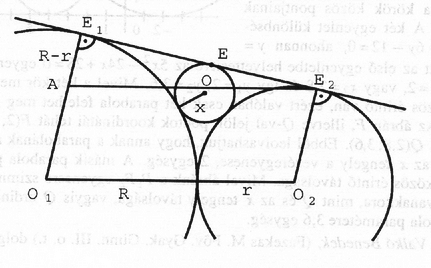