Feladat: F.2984 Korcsoport: 18- Nehézségi fok: átlagos
Megoldó(k):  Valkó Benedek 
Füzet: 1994/október, 359 - 360. oldal  PDF  |  MathML 
Témakör(ök): Másodfokú (és arra visszavezethető) egyenletrendszerek, Kör egyenlete, Parabola egyenlete, Feladat
Hivatkozás(ok):Feladatok: 1993/november: F.2984

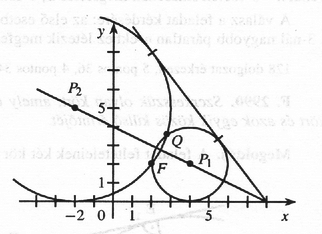
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A parabola definíciója szerint a feladatban említett két parabola egyikének vezéregyenese a P1 és P2 középpontú P1F, illetve P2F sugarú körök egyik közös érintője, a másik parabola vezéregyenese pedig a másik közös érintő (lásd az ábrát), feltéve, hogy csak két közös érintő van. Könnyen láthatjuk, hogy a két kör egyik közös érintője az x tengely. A körök egyenlete:

(x+2)2+(y-5)2=25,

illetve
(x-4)2+(y-2)2=4.

Ezekből az egyenletekből
x2+4x+y2-10y+4=0,x2-8x+y2-4y+16=0.

Ennek az egyenletrendszernek a megoldásai a körök közös pontjainak koordinátái. A két egyenlet különbségéből 12x-6y-12=0, ahonnan y=2x-2. Ezt az első egyenletbe helyettesítve az 5x2-24x+12=0 egyenletet kapjuk, amelyből x1=2, vagy x2=2,8 és így y1=2; y2=3,6. Mivel a két kör metszi egymást, csak két közös érintő van, ezért valóban csak két parabola felelhet meg a feladat feltételeinek. Az ábrán F, illetve Q-val jelölt pontok koordinátái tehát F(2;2), amint ezt tudtuk is, és Q(2,8;3,6). Ebből leolvashatjuk, hogy annak a parabolának a paramétere, amelyiknek az x tengely a vezéregyenese, 2 egység. A másik parabola paramétere F és a másik közös érintő távolsága. Mival ábránk a P1P2 egyenesre szimmetrikus, ez a távolság ugyanakkora, mint Q és az x tengely távolsága, vagyis Q ordinátája. Ezért a másik parabola paramétere 3,6 egység.
Valkó Benedek (Fazekas M. Főv. Gyak. Gimn., III. o. t.) dolgozata alapján